
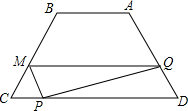
 如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同的速度从点D出发沿DA方向向终点A运动,进点Q作QM∥CD交BC于点M,连接MP(其中一个动点到达端点时,另一个动点也随之停止运动).设CP=x
如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同的速度从点D出发沿DA方向向终点A运动,进点Q作QM∥CD交BC于点M,连接MP(其中一个动点到达端点时,另一个动点也随之停止运动).设CP=x分析 (1)如图过A作AE⊥CD,垂足为E.则DE=$\frac{1}{2}$(CD-AB)据此即可求得DE的长,然后在直角△ADE中,利用三角函数即可求解;
(2)分成∠PQD=90°,和∠QPD=90°两种情况进行讨论,当∠PQD=90°,有PD=2DQ,当∠DPQ=90°,有DQ=2PD,据此即可列方程求解,进行判断;
(3)易证四边形MCDQ是等腰梯形,则△CPM恰为等边三角形,四边形PDQM是平行四边形,则当PD=DQ时□PDQM是菱形,根据PD=DQ即可列方程求得CP的长.
解答 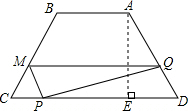 解:(1)如图过A作AE⊥CD,垂足为E.
解:(1)如图过A作AE⊥CD,垂足为E.
依题意,DE=9$\frac{9-4}{2}$=$\frac{5}{2}$.
在Rt△ADE中,AD=$\frac{DE}{cos60°}$=$\frac{5}{2}$×2=5.
(2)∵∠D=60°.
当∠PQD=90°,有PD=2DQ,9-x=2x,x=3,
当∠DPQ=90°,有DQ=2PD,x=2(9-x),x=6>5,不可能.
∴x=3时,△PDQ为直角三角形.
(3)四边形PDQM能成为菱形.
理由是:∵QM∥DC,∠C=∠D,
∴四边形MCDQ是等腰梯形,
∴MC=DQ=CP,
∴∠C=60°
∴△CPM恰为等边三角形
∴∠1=∠D=60°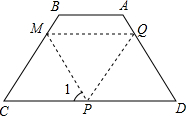
∴MP∥QD,
∵QM∥DC,
∴四边形PDQM是平行四边形.
当PD=DQ时,□PDQM是菱形.
此时,由 PD=DQ,得9-x=x,x=$\frac{9}{2}$.
点评 本题是等腰梯形以及等边三角形以及菱形的判定的综合应用,正确确定四边形PDQM是菱形的条件是关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:选择题
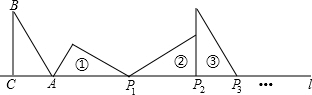
| A. | 2012+671$\sqrt{3}$ | B. | 2013+671$\sqrt{3}$ | C. | 2014+671$\sqrt{3}$ | D. | 2015+671$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com