
【题目】在平面直角坐标系中,抛物线![]() 的图像与x轴交于B,C两点(B在C的左侧),与y轴交于点A。
的图像与x轴交于B,C两点(B在C的左侧),与y轴交于点A。
(1)求出点A,B,C的坐标。
(2)向右平移抛物线,使平移后的抛物线恰好经过△ABC的外心,求出平移后的抛物线的解析式.
【答案】(1)A(0,4), B(-2,0), C(8,0) ;(2) ![]()
【解析】
(1)根据二次函数与一元二次方程的关系,令y=0,可得:,![]() ,解得:
,解得:![]() ,继而求出B(-2,0), C(8,0), 令x=0,则y=4,继而求出A(0,4),
,继而求出B(-2,0), C(8,0), 令x=0,则y=4,继而求出A(0,4),
(2) 根据![]() ,因此可得:
,因此可得:![]() ,根据勾股定理逆定理可得:△ABC是直角三角形,根据直角三角形性质可得:△ABC的外心为(3,0),
,根据勾股定理逆定理可得:△ABC是直角三角形,根据直角三角形性质可得:△ABC的外心为(3,0),
再根据二次函数图象平移可得:抛物线向右平移5个单位,平移后的抛物线为:![]() .
.
(1)A(0,4), B(-2,0), C(8,0),
(2) ∵![]() ,
,
∴![]() ,
,
∴△ABC是直角三角形,
∴△ABC的外心为(3,0),
∴抛物线向右平移5个单位,
平移后的抛物线为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某项工程由甲乙两队合作12天可以完成,供需工程费用13800元,乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多150元。
(1)甲乙两队单独完成这项工程分别需要多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成这项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一客车一出租车分别从甲乙两地相向而行同时出发,设客车离甲地距离为y1千米,出租车离甲地距离为y2千米,两车行驶的时间为x小时,y1、y2关于的函数图象如图所示:

(1)根据图象,直接写出y1、y2关于x的关系式;
(2)求经过多少小时,两车之间的距离为120千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推、则正方形OB2018B2019C2019的顶点B2019的坐标是______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办了绿色阅读节活动,为了表彰优秀,陈老师负责购买奖品,在购买时他发现身上所带的钱:若以2支钢笔和3个笔记本为一份奖品,则可买50份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品,设钢笔单价为![]() 元/支,笔记本单价为
元/支,笔记本单价为![]() 元/支.
元/支.
(1)请用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)若用这笔钱全部购买笔记本,总共可以买几本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)试说明△ABC是等腰三角形;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒2cm的速度沿线段BA向点A 运动,同时动点N从点A出发以每秒1cm速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.
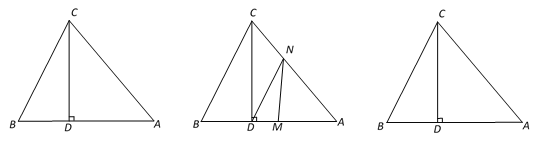
图1 图2 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系![]() 中
中![]() ,
,![]() ,
,![]() .
.

(1)作出![]() 关于直线
关于直线![]() 对称的图形△
对称的图形△![]() 并写出△
并写出△![]() 各顶点的坐标;
各顶点的坐标;
(2)将△![]() 向左平移2个单位,作出平移后的△
向左平移2个单位,作出平移后的△![]() ,并写出△
,并写出△![]() 各顶点的坐标;
各顶点的坐标;
(3)观察![]() 和△
和△![]() ,它们是否关于某直线对称?若是,请指出对称轴,并求
,它们是否关于某直线对称?若是,请指出对称轴,并求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com