
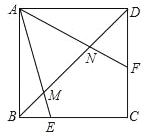
【题目】如图,正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,若DN=1,BM=2,那么MN=_____.证明:DN2+BM2=MN2.
【答案】![]()
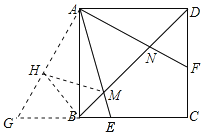
【解析】解:如图,延长CB到G,使BG=DF,连接AG,在AG截取AH=AN,连接MH、BH.∵四边形ABCD为正方形,∴AB=BC=CD=AD,∠BDC=∠ABD=45°,∠BAD=∠ADF=∠ABE=∠ABG=90°.在△ABG和△ADF中, ,∴△ABG≌△ADF(SAS),∴∠BAG=∠DAF,∠AFD=∠G,AF=AG,∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠BAD﹣∠EAF=90°﹣45°=45°=∠EAF.在△AMN和△AMH中,
,∴△ABG≌△ADF(SAS),∴∠BAG=∠DAF,∠AFD=∠G,AF=AG,∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠BAD﹣∠EAF=90°﹣45°=45°=∠EAF.在△AMN和△AMH中,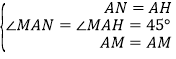 ,∴△AMN≌△AMH(SAS),∴MN=MH.∵AF=AG,AN=AH,∴FN=AF﹣AN=AG﹣AH=GH.在△DFN和△BGH中,
,∴△AMN≌△AMH(SAS),∴MN=MH.∵AF=AG,AN=AH,∴FN=AF﹣AN=AG﹣AH=GH.在△DFN和△BGH中,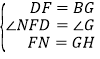 ,∴△DFN≌△BGH(SAS),∴∠GBH=∠NDF=45°,DN=BH,∴∠MBH=∠ABH+∠ABD=∠ABG﹣∠GBH+∠ABD=90°﹣45°+45°=90°,∴BM2+DN2=BM2+BH2=MH2=MN2.
,∴△DFN≌△BGH(SAS),∴∠GBH=∠NDF=45°,DN=BH,∴∠MBH=∠ABH+∠ABD=∠ABG﹣∠GBH+∠ABD=90°﹣45°+45°=90°,∴BM2+DN2=BM2+BH2=MH2=MN2.
当DN=1,BM=2时,12+22=MN2,∴MN=![]() .∵MN>0,∴MN=
.∵MN>0,∴MN=![]() .
.
故答案为:![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′(不写画法);
(2)并直接写出点B′、C′的坐标:B′( )、C′( );
(3)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
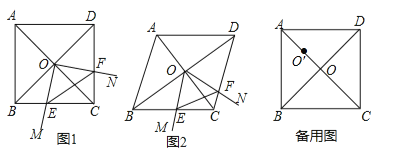
【题目】(12分)菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且![]() 时,直接写出线段CE的长.
时,直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
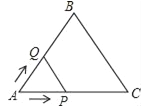
【题目】如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB﹣BC向点C运动,到达点C停止,设△APQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A. 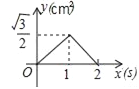 B.
B. 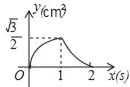
C. 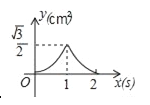 D.
D. 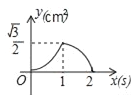
查看答案和解析>>
科目:初中数学 来源: 题型:
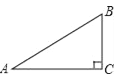
【题目】某校计划把一块近似于直角三角形的废地开发为生物园,如图所示,∠ACB=90°,BC=60米,∠A=36°.
(1)若入口处E在AB边上,且与A、B等距离,求CE的长(精确到个位);
(2)若D点在AB边上,计划沿线段CD修一条水渠.已知水渠的造价为50元/米,水渠路线应如何设计才能使造价最低,求出最低造价.
(其中sin36°=0.5878,cos36°=0.8090,tan36°=0.7265)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

【答案】(1)b=﹣2a,顶点D的坐标为(﹣![]() ,﹣
,﹣![]() );(2)
);(2)![]() ;(3) 2≤t<
;(3) 2≤t<![]() .
.
【解析】试题分析:(1)把M点坐标代入抛物线解析式可得到b与a的关系,可用a表示出抛物线解析式,化为顶点式可求得其顶点D的坐标;
(2)把点![]() 代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得
代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得![]() 的面积即可;
的面积即可;
(3)先根据a的值确定抛物线的解析式,画出图2,先联立方程组可求得当GH与抛物线只有一个公共点时,t的值,再确定当线段一个端点在抛物线上时,t的值,可得:线段GH与抛物线有两个不同的公共点时t的取值范围.
试题解析:(1)∵抛物线![]() 有一个公共点M(1,0),
有一个公共点M(1,0),
∴a+a+b=0,即b=2a,
![]()
∴抛物线顶点D的坐标为![]()
(2)∵直线y=2x+m经过点M(1,0),
∴0=2×1+m,解得m=2,
∴y=2x2,
则![]()
得![]()
∴(x1)(ax+2a2)=0,
解得x=1或![]()
∴N点坐标为![]()
∵a<b,即a<2a,
∴a<0,
如图1,设抛物线对称轴交直线于点E,

∵抛物线对称轴为![]()
![]()
![]()
设△DMN的面积为S,
![]()
(3)当a=1时,
抛物线的解析式为:![]()
有![]()
![]()
解得:![]()
∴G(1,2),
∵点G、H关于原点对称,
∴H(1,2),
设直线GH平移后的解析式为:y=2x+t,
x2x+2=2x+t,
x2x2+t=0,
△=14(t2)=0,
![]() 当点H平移后落在抛物线上时,坐标为(1,0),
当点H平移后落在抛物线上时,坐标为(1,0),
把(1,0)代入y=2x+t,
t=2,
∴当线段GH与抛物线有两个不同的公共点,t的取值范围是![]()

【题型】解答题
【结束】
24
【题目】在△ABC中,AB=AC,点D是直线BC上的一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE,设∠BAC=α,∠BCE=β.
(1)如图①,当点D在线段BC上,如果α=60°,β=120°;
如图②,当点D在线段BC上,如果α=90°,β=90°
如图③,当点D在线段BC上,如果α,β之间有什么样的关系?请直接写出.
(2)如图④,当点D在射线BC上,(1)中结论是否成立?请说明理由.
(3)如图⑤,当点D在射线CB上,且在线段BC外,(1)中结论是否成立?若不成立,请直接写出你认为正确的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
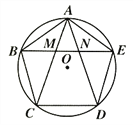
【题目】如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AMAD;③MN=3-![]() ;④S△EBC=2
;④S△EBC=2![]() -1,其中正确的结论是_________(把你认为正确结论的序号都填上).
-1,其中正确的结论是_________(把你认为正确结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com