练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图 ，在矩形ABCD中 ，AB=10 , BC=5 ． 若点M、N分别是线段AC、AB上的两个动点，则BM+MN的最小值为（   ）                                                                                                                                    

    A． 10        B．  8           C．            D． 6         


    B


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若a>0,b>0,且+=.

    (1) 求a3+b3的最小值;

    (2)是否存在a,b,使得2a+3b=6?并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∠BOC=60°，顶点C的坐标为（m,3），反比例函数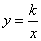的图像与菱形对角线AO交于D点，连接BD，当BD⊥x轴时，k的值是（     ）   

           

    A．6    B．－6    C．12    D．－12

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形ABCD中，点P在边CD上，且与C、D不重合，过点A作AP的垂线与CB的延长线相交于点Q，连接PQ，M为PQ中点．

    （1）求证：△ADP∽△ABQ；

    （2）若AD=10，AB=20，点P在边CD上运动，设DP=x，BM2=y，求y与x的函数关系式，并求线段BM的最小值；

    （3）若AD=10，AB=a，DP=8，随着a的大小的变化，点M的位置也在变化．当点M落在矩形ABCD外部时，求a的取值范围．




    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知∠1＝∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是(　　)

    A．＝          B．＝     C．∠B＝∠D        D．∠C＝∠AED

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC∽△DEF，且相似比是3：4，△ABC的面积是18cm2，则△DEF的面积为___________cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


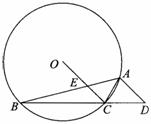
    如图所示，⊙O的内接△ABC中，∠BAC＝45°，∠ABC＝15°，AD∥OC并交BC的延长线于D点，OC交AB于E点．

    (1)求∠D的度数；

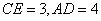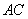    (2)若,求线段的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


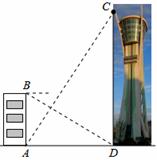
    ．观光塔是潍坊市区的标志性建筑，为测量其高度，如图，一人先在附近一楼房的底端A点观测观光塔顶端C处的仰角是60°，然后爬到该楼房顶端B处观测观光塔底部D处的俯角是30°，已知楼房高AB约是45 m，根据以上观测数据可求观光塔的高CD是       m．

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若，则a+b=　　　　　　。

    查看答案和解析>>

    同步练习册答案