
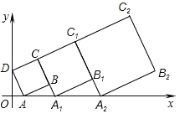
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2012个正方形的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先根据两对对应角相等的三角形相似,证明△AOD和△A1BA相似,根据相似三角形对应边成比例可以得到AB=2A1B,所以正方形A1B1C1C的边长等于正方形ABCD边长的![]() ,以此类推,后一个正方形的边长是前一个正方形的边长的
,以此类推,后一个正方形的边长是前一个正方形的边长的![]() ,然后即可求出第2014个正方形的边长与第1个正方形的边长的关系,从而求出第2012个正方形的面积.
,然后即可求出第2014个正方形的边长与第1个正方形的边长的关系,从而求出第2012个正方形的面积.
解:如图,
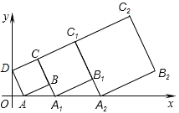
∵四边形ABCD是正方形,
∴∠ABC=∠BAD=90°,AB=BC,
∴∠ABA1=90°,∠DAO+∠BAA1=90°,
又∵在坐标平面内,∠DAO+∠ADO=90°,
∴∠ADO=∠BAA1,
在△AOD和△A1BA中,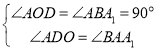 ,
,
∴△AOD∽△A1BA,
∴OD:AO=AB:A1B=2,
∴BC=2A1B,
∴A1C=![]() BC,
BC,
以此类推A2C1=![]() A1C,A3C2=
A1C,A3C2=![]() A2C1,…,
A2C1,…,
即后一个正方形的边长是前一个正方形的边长的![]() 倍,
倍,
∴第2012个正方形的边长为(![]() )2011BC,
)2011BC,
∵A的坐标为(1,0),D点坐标为(0,2),
∴BC=AD=![]() ,
,
∴第2012个正方形的面积为:[(![]() )2011BC]2=5×(
)2011BC]2=5×(![]() )4022.
)4022.
故选:D.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
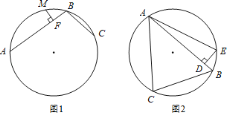
【题目】定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.阿基米德折弦定理:如图1,AB和BC组成圆的折弦,AB>BC,M是弧ABC的中点,MF⊥AB于F,则AF=FB+BC.
如图2,△ABC中,∠ABC=60°,AB=8,BC=6,D是AB上一点,BD=1,作DE⊥AB交△ABC的外接圆于E,连接EA,则∠EAC=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
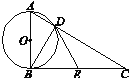
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,E是BC的中点,连接BD,DE.
(1)若![]() ,求sinC;
,求sinC;
(2)求证:DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,抛物线![]() 与x轴交于A,B两点,点P在该抛物线上(P点与A. B两点不重合),如果△ABP中PA与PB两条边的三边满足其中一边是另一边
与x轴交于A,B两点,点P在该抛物线上(P点与A. B两点不重合),如果△ABP中PA与PB两条边的三边满足其中一边是另一边![]() 倍,则称点P为抛物线
倍,则称点P为抛物线![]() 的“好”点.
的“好”点.
(1)命题:P(0,3)是抛物线![]() 的“好”点.该命题是_____( 真或假)命题.
的“好”点.该命题是_____( 真或假)命题.
(2)如图2,已知抛物线C:![]() 与
与![]() 轴交于A,B两点,点P(1,2)是抛物线C的“好”点,求抛物线C的函数表达式.
轴交于A,B两点,点P(1,2)是抛物线C的“好”点,求抛物线C的函数表达式.
(3)在(2)的条件下,点Q在抛物线C上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参与两个数学活动,再回答问题:
活动![]() :观察下列两个两位数的积
:观察下列两个两位数的积![]() 两个乘数的十位上的数都是9,个位上的数的和等于
两个乘数的十位上的数都是9,个位上的数的和等于![]() ,猜想其中哪个积最大?
,猜想其中哪个积最大?
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
活动![]() :观察下列两个三位数的积
:观察下列两个三位数的积![]() 两个乘数的百位上的数都是9,十位上的数与个位上的数组成的数的和等于
两个乘数的百位上的数都是9,十位上的数与个位上的数组成的数的和等于![]() ,猜想其中哪个积最大?
,猜想其中哪个积最大?
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 分别写出在活动
分别写出在活动![]() 、
、![]() 中你所猜想的是哪个算式的积最大?
中你所猜想的是哪个算式的积最大?
![]() 对于活动
对于活动![]() ,请用二次函数的知识证明你的猜想.
,请用二次函数的知识证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
在数学活动课上,老师给出如下问题,让同学们展开探究活动:
[问题情境]
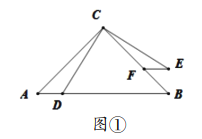
如图①,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上一点
上一点![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到的对应线段为
,得到的对应线段为![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,请你根据上述条件,提出恰当的数学问题并解答.
,请你根据上述条件,提出恰当的数学问题并解答.
[解决问题]
下面是学习小组提出的三个问题,请你解答这些问题:
(1)“兴趣”组提出的问题是:求证:![]() ;
;
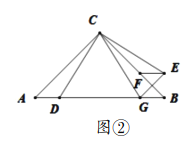
(2)“实践”小组提出的问题是:如图②,若将![]() 沿
沿![]() 的垂直平分线对折,得到
的垂直平分线对折,得到![]() ,连接
,连接![]() ,则线段
,则线段![]() 与
与![]() 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;
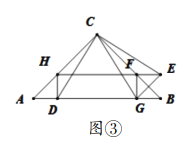
(3)“奋进”小组在“实践”小组探究的基础上,提出了如下问题:延长![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,求证:四边形
,求证:四边形![]() 是矩形.
是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,∠E=30°,AC=5.
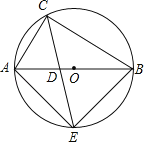
(1)求CE的长;
(2)求S△ADC:S△ACE的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
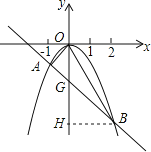
【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx﹣2的图象相交于A、B两点,如图所示,其中A(﹣1,﹣1),
(1)求二次函数和一次函数解析式.
(2)求△OAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com