练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算： +（ ）﹣1﹣2cos60°+（3﹣π）0 ．

    【答案】解： +（ ）﹣1﹣2cos60°+（3﹣π）0
    =2+2﹣1+1
    =4
    【解析】直接利用负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值以及二次根式的性质分别化简各数，进而得出答案．
    【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点，需要掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，船A、B在东西方向的海岸线MN上，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东60°方向上，在船B的北偏西37°方向上，AP=30海里．

    （1）尺规作图：过点P作AB所在直线的垂线，垂足为E（要求：保留作图痕迹，不写作法）；
    （2）求船P到海岸线MN的距离（即PE的长）；
    （3）若船A、船B分别以20海里/时、15海里/时的速度同时出发，匀速直线前往救援，试通过计算判断哪艘船先到达船P处．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的袋子中有5个完全相同的小球，球上分别标着点A（-2，0），B（1，0），C（4，0），D（0，-6），E（-2，3）．从袋子中一次性随机摸出3个球，这3个球分别代表的点恰好能确定一条抛物线（对称轴平行于y轴）的概率是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知⊙O的半径为5，且点O在直线l上，小明用一个三角板学具（∠ABC=90°，AB=BC=8）做数学实验：
    （1）如图①，若A、B两点在⊙O上滑动，直线BC分别与⊙O，L相交于点D，E．
    ①求BD的长；②当OE=6时，求BE的长；

    （2）如图②，当点B在直线l上，点A在⊙O上，BC与⊙O相切于点P时，则切线长PB=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB为⊙O的直径，F为⊙O上一点，AC平分∠BAF且交⊙O于点C，过点C作CD⊥AF于点D，延长AB、DC交于点E，连接BC，CF．

    （1）求证：CD是⊙O的切线；
    （2）若AD=6，DE=8，求BE的长；
    （3）求证：AF+2DF=AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数y=x2+bx+c的图象与x轴交于A，B两点，与y轴交于点P，顶点为C（1，﹣2）．

    （1）求此函数的关系式；
    （2）作点C关于x轴的对称点D，顺次连接A，C，B，D．若在抛物线上存在点E，使直线PE将四边形ACBD分成面积相等的两个四边形，求点E的坐标；
    （3）在（2）的条件下，抛物线上是否存在一点F，使得△PEF是以P为直角顶点的直角三角形？若存在，求出点F的坐标及△PEF的面积；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，一幢楼房AB背后有一台阶CD，台阶每层高0.2米，且AC=17.2米，设太阳光线与水平地面的夹角为α，当α=60°时，测得楼房在地面上的影长AE=10米，现有一只小猫睡在台阶的MN这层上晒太阳．（ 取1.73）

    （1）求楼房的高度约为多少米？
    （2）过了一会儿，当α=45°时，问小猫能否还晒到太阳？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A是直线l外一点，在l上取两点B，C，分别以A，C为圆心，BC，AB的长为半径作弧，两弧交于点D，分别连接AB，AD，CD，若∠ABC+∠ADC=120°，则∠A的度数是（ ）

    A.100°
    B.110°
    C.120°
    D.125°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE=DF．给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC；从中选择一个条件使四边形BECF是菱形，你认为这个条件是（只填写序号）．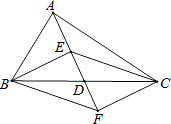

    查看答案和解析>>

    同步练习册答案