
【题目】如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC,CF. 
(1)求证:CD是⊙O的切线;
(2)若AD=6,DE=8,求BE的长;
(3)求证:AF+2DF=AB.
【答案】
(1)解:
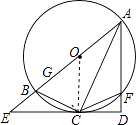
连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵CD⊥AF,
∴∠D=90°,
∴∠ACB=∠D,
∵AC平分∠BAF,
∴∠BAC=∠CAD,
∴△ABC∽△ACD,
∴∠ABC=∠ACD,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠ACD,
∵∠OCB+∠ACO=∠ACO+∠ACD=90°,
∴∠OCD=90°,
∴CD是⊙O的切线
(2)解:∵AD=6,DE=8,
∴AE= ![]() =10,
=10,
∵OC∥AD,
∴∠OCE=∠ADE,
∴△OCE∽△ADE,
∴ ![]() ,
,
即 ![]() ,
,
∴r= ![]() ,
,
∴BE=10﹣ ![]() =
= ![]()
(3)解:过C作 CG⊥AE于G,
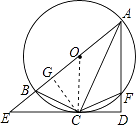
在△ACG与△ACD中,
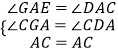 ,
,
∴△ACG≌△ACD,
∴AG=AD,CG=CD,
∵BC=CF,
在Rt△BCG与Rt△FCD中,
![]() ,
,
∴Rt△BCG≌Rt△FCD,
∴BG=FD,
∴AF+2DF=AD+DF=AG+GB=AB,
即AF+2DF=AB.
【解析】(1)连接OC,由AB为⊙O的直径,得到∠ACB=90°,求得∠ACB=∠D,根据角平分线的性质得到∠BAC=∠CAD,通过相似三角形得到∠ABC=∠ACD,等量代换得到∠OCB=∠ACD,求出∠OCD=90°,即可得到结论;(2)根据勾股定理得到AE= ![]() =10,根据相似三角形的性质得到
=10,根据相似三角形的性质得到 ![]() ,代入数据得到r=
,代入数据得到r= ![]() ,于是得到结论;(3)过C作 CG⊥AE于G,根据全等三角形的性质得到AG=AD,CG=CD,推出Rt△BCG≌Rt△FCD,由全等三角形的性质得到BG=FD,等量代换即可得到结论.
,于是得到结论;(3)过C作 CG⊥AE于G,根据全等三角形的性质得到AG=AD,CG=CD,推出Rt△BCG≌Rt△FCD,由全等三角形的性质得到BG=FD,等量代换即可得到结论.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为( ![]() ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( ) 
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“上海迪士尼乐园”将于2016年6月16日开门迎客,小明准备利用暑假从距上海2160千米的某地去“上海迪士尼乐园”参观游览,下图是他在火车站咨询得到的信息: 
根据上述信息,求小明乘坐城际直达动车到上海所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外活动小组采用简单随机抽样的方法,对本校九年级学生的睡眠时间(单位:h)进行了调查,并将所得数据整理后绘制出频数分布直方图的一部分(如图).设图中从左至右前5个小组的频率分别是0.04,0.08,0.24,0.28,0.24,第2小组的频数为4.(每组只含最小值,不含最大值) 
(1)该课外活动小组抽取的样本容量是多少?请补全图中的频数分布直方图;
(2)样本中,睡眠时间在哪个范围内的人数最多?这个范围的人数是多少?
(3)设该校九年级学生900名,若合理的睡眠时间范围为7≤h<9,你对该校九年级学生的睡眠时间做怎样的分析、推断?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合. 
(1)将△ABC向右平移3个单位长度,得到△DEF(A与D、B与E、C与F对应),请在方格纸中画出△DEF;
(2)在(1)的条件下,连接AE和CE,请直接写出△ACE的面积S,并判断B是否在边AE上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com