
分析 设抛物线与x轴的一个交点是(t,0),根据交点式得到抛物线解析式为y=(x-3+$\sqrt{2}$)(x-t),再把解析式化为一般式后可得m=-(3-$\sqrt{2}$+t),(3-$\sqrt{2}$)t=7,然后求出t,再计算出m的值即可.
解答 解:设抛物线与x轴的一个交点是(t,0),
设抛物线解析式为y=(x-3+$\sqrt{2}$)(x-t),
即y=x2-(3-$\sqrt{2}$+t)x+(3-$\sqrt{2}$)t,
所以m=-(3-$\sqrt{2}$+t),(3-$\sqrt{2}$)t=7,
解得t=3+$\sqrt{2}$,m=-(3-$\sqrt{2}$+3+$\sqrt{2}$)=-6,
所以m的值为-6,另一个交点坐标,为(3+$\sqrt{2}$,0).
点评 本题考查了抛物线与x轴的交点:从二次函数的交点式y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)中可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).


科目:初中数学 来源: 题型:填空题
 如图,点A、B在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,将该函数图象向上平移1个单位长度得到一条新的曲线,点A,B的对应点分别为A′、B′.若A(m,4),B′(6,3),则曲线线段AB扫过的阴影部分的面积为3.
如图,点A、B在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,将该函数图象向上平移1个单位长度得到一条新的曲线,点A,B的对应点分别为A′、B′.若A(m,4),B′(6,3),则曲线线段AB扫过的阴影部分的面积为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
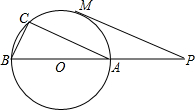 如图,直线PO交⊙O于A,B两点,直径AB=10,弦AC∥PM.点M是$\widehat{AC}$的中点,
如图,直线PO交⊙O于A,B两点,直径AB=10,弦AC∥PM.点M是$\widehat{AC}$的中点,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°,…照这样走下去,他第一次回到出发地A点时,一共走了180米.
如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°,…照这样走下去,他第一次回到出发地A点时,一共走了180米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,分别交AB,AC于点E,D.
如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,分别交AB,AC于点E,D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在下列解答中,填写适当的理由或数学式:
如图,在下列解答中,填写适当的理由或数学式:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,某城市十字路口旁有一居民区A,现在城市规划局想建设两个公交车站以方便小区居民的工作与生活,那么两车站应建在什么位置最合适呢?请你在图中画出来.
如图所示,某城市十字路口旁有一居民区A,现在城市规划局想建设两个公交车站以方便小区居民的工作与生活,那么两车站应建在什么位置最合适呢?请你在图中画出来.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com