
【题目】如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O. 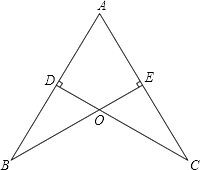
(1)求证:AD=AE;
(2)试猜想:OA与BC的位置关系,并加以证明.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
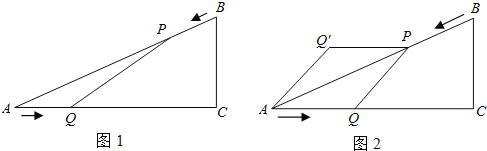
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6 cm ,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm /s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.
(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?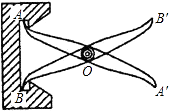
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.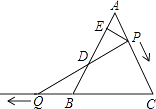
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.明天太阳从西方升起
B.打开电视机,正在播放广告
C.掷一枚硬币,正面朝上
D.任意一个三角形,它的内角和等于180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若( ![]() ☆3)☆(﹣
☆3)☆(﹣ ![]() )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m,( ![]() x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE. 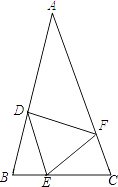
(1)求证:△DEF是等腰三角形;
(2)求证:∠B=∠DEF;
(3)当∠A=40°时,求∠DEF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com