【题目】如图，在矩形ABCD中，AB=5，BC=10 
，一圆弧过点B和点C，且与AD相切，则图中阴影部分面积为 ． 
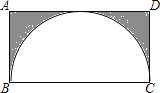
【答案】75 
﹣ 
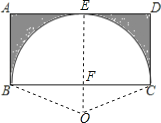
【解析】解：设圆弧的圆心为O，与AD切于E，
连接OE交BC于F，连接OB、OC，
设圆的半径为x，则OF=x﹣5，
由勾股定理得，OB2=OF2+BF2 ，
即x2=（x﹣5）2+（5 ）2 ，
解得，x=5，
则∠BOF=60°，∠BOC=120°，
则阴影部分面积为：矩形ABCD的面积﹣（扇形BOCE的面积﹣△BOC的面积）
=10 ×5﹣ 
+ 
×10 ×5=75 ﹣ ，
所以答案是：75 ﹣ ．
【考点精析】本题主要考查了矩形的性质和切线的性质定理的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．
同步奥数系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知抛物线y=x2+bx+c过A，B，C三点，点A的坐标是（3，0），点C的坐标是（0，﹣3），动点P在抛物线上．
（1）b= ， c= ， 点B的坐标为；（直接填写结果）
（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；
（3）过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，向一个半径为R、容积为V的球形容器内注水，则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是（ ）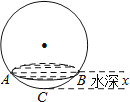 
A.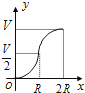
B.
C.
D.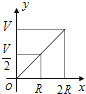
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（－1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．
（1）求点C，D的坐标及平行四边形ABDC的面积
.
（2）在y轴上是否存在一点P，连接PA，PB，使
＝2，若存在这样一点，求出点P的坐标，若不存在，试说明理由．
（3）点P是四边形ABCD边上的点，若△OPC为等腰三角形时，直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以下列数组作为三角形的三条边长，其中能构成直角三角形的是( )
A. 1， 
，3 B. 
， 
，5 C. 1.5，2，2.5 D. 
， 
， 
【答案】C
【解析】A、12+（
）2≠32，不能构成直角三角形，故选项错误；
B、(
2+（
）2≠52，不能构成直角三角形，故选项错误；
C、1.52+22=2.52，能构成直角三角形，故选项正确；
D、（
））2+（
）2≠（
）2，不能构成直角三角形，故选项错误．
故选：C．
【题型】单选题
【结束】
3
【题目】在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到斜边AB的距离是（ ）
（A）
（B）
（C）9 （D）6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，已知△ABC，以AB、AC为边分别向外作正方形ABFD和正方形ACGE，连结BE、CD，猜想BE与CD有什么数量关系？并说明理由；
（2）请模仿正方形情景下构造全等三角形的思路，利用构造全等三角形完成下题：如图2，要测量池塘两岸相对的两点B、E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长（结果保留根号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E．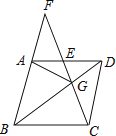
（1）求证：AG=CG．
（2）求证：AG2=GEGF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的网格中，线段AB和直线a如图所示，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在格点上．
（1）在图中画出以线段AB为一边的正方形 ABCD，且点C和点D均在格点上，
并直接写出正方形 ABCD的面积为 ；
（2）在图中以线段AB为一腰的等腰三角形ABE，点E在格点上，则满足条件的点E有_____ 个；
（3）在图中的直线a上找一点Q，使得△QAB的周长最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
