
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 顶点为
顶点为![]() ,且该抛物线与
,且该抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧).我们规定:抛物线与
的左侧).我们规定:抛物线与![]() 轴围成的封闭区域称为“
轴围成的封闭区域称为“![]() 区域”(不包含边界);横、纵坐标都是整数的点称为整点.
区域”(不包含边界);横、纵坐标都是整数的点称为整点.
(1)求抛物线![]() 顶点
顶点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)如果抛物线![]() 经过
经过![]() .
.
①求![]() 的值;
的值;
②在①的条件下,直接写出“![]() 区域”内整点的个数.
区域”内整点的个数.
(3)如果抛物线![]() 在“
在“![]() 区域”内有4个整点,直接写出
区域”内有4个整点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②6个;(3)
;②6个;(3)![]() 或
或![]() .
.
【解析】
(1)将抛物线![]() 改写为顶点式,即可得到顶点坐标;
改写为顶点式,即可得到顶点坐标;
(2)①将(1,3)代入![]() ,即可求出
,即可求出![]() 的值;②根据函数图像可判断出整数的个数;
的值;②根据函数图像可判断出整数的个数;
(3)分![]() 和
和![]() 两种情况讨论,根据有4个整点画出图像,可求出
两种情况讨论,根据有4个整点画出图像,可求出 ![]() 的取值范围.
的取值范围.
(1)∵![]() ,
,
∴该抛物线的顶点为![]() .
.
(2)①∵抛物线![]() 经过
经过![]() ,
,
∴![]() ,解得
,解得![]() .
.
②当![]() 时,
时,![]() ,
,
令y=0,则![]() ,解得
,解得![]() ,
,![]() ,
,
设抛物线与x轴交于A、B两点,则A(-1,0),B(3,0),抛物线图像如下图所示,
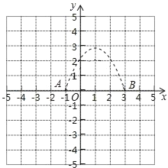
当![]() 时,
时,![]() ,所以(0,1)和(0,2)两个整数点在“
,所以(0,1)和(0,2)两个整数点在“![]() 区域”,
区域”,
当![]() 时,
时,![]() ,所以(1,1)和(1,2)两个整数点在“
,所以(1,1)和(1,2)两个整数点在“![]() 区域”,
区域”,
当![]() 时,
时,![]() ,所以(2,1)和(2,2)两个整数点在“
,所以(2,1)和(2,2)两个整数点在“![]() 区域”,
区域”,
综上所述,此“![]() 区域”内整点的个数为6个.
区域”内整点的个数为6个.
(3)当![]() 时,
时,![]() ,
,
∴抛物线与y轴的交点为(0,-3a),
当![]() 时,
时,![]()
当![]() 时,
时,![]()
若![]() ,则函数图像如下图所示,
,则函数图像如下图所示,
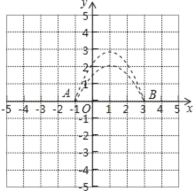
由图像可知,如果抛物线![]() 在“
在“![]() 区域”内有4个整点,
区域”内有4个整点,
则![]() ,解得:
,解得:![]() ;
;
若![]() ,则函数图像如下图所示,
,则函数图像如下图所示,
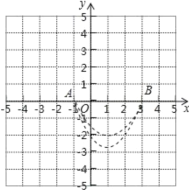
由图像可知,如果抛物线![]() 在“
在“![]() 区域”内有4个整点,
区域”内有4个整点,
则![]() ,解得:
,解得:![]() .
.
综上所述,如果抛物线![]() 在“
在“![]() 区域”内有4个整点,则
区域”内有4个整点,则![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
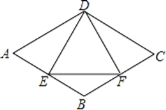
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3
B.4
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的上地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏50米,设AB的长为x米,长方形的面积为y平方米.
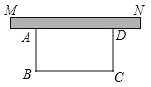
(1)请求出y与x的函数关系式(不需写出自变量的取值范围)
(2)不考虑墙体长度,问AB的长为多少时,长方形的面积最大?
(3)若墙体长度为20米,问长方形面积最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)小亮遇到了这样一道题:已知如图在![]() 中,
中,![]() 在
在![]() 上,
上,![]() 在
在![]() 的延长上,
的延长上,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
小亮仔细分析了题中的已知条件后,如图②过![]() 点作
点作![]() 交
交![]() 于
于![]() ,进而解决了该问题.(不需要证明)
,进而解决了该问题.(不需要证明)
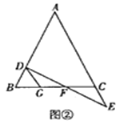
(探究)如图③,在四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 边的中点,
边的中点,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,试探究线段
,试探究线段![]() 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
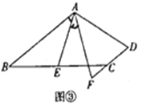
(应用)如图③,在正方形![]() 中,
中,![]() 为
为![]() 边的中点,
边的中点,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 边上的点,若
边上的点,若![]() =1,
=1,![]() =
=![]() ,∠
,∠![]() =90°,则
=90°,则![]() 的长为 .
的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
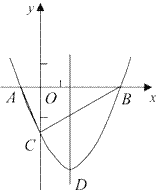
【题目】如图,抛物线y=![]() x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.

(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
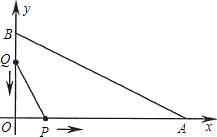
【题目】在平面直角坐标系中,已知OA=10cm,OB=5cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤5),
(1)用含t的代数式表示:线段PO= cm;OQ= cm.
(2)当t为何值时,四边形PABQ的面积为19cm2.
(3)当△POQ与△AOB相似时,求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC角AD边于点F,连结BD.
(1)求证:四边形EFCD是正方形;
(2)若BE=1,ED=2![]() ,求BD的长.
,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
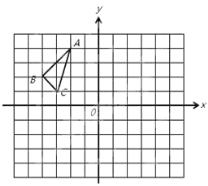
【题目】△ABC 在平面直角坐标系中的位置如图所示,其中每 个小正方形的边长为 1 个单位长度.
(1)画出△ABC 关于原点 O 的中心对称图形△A1B1C1,并写出点 A1 的坐标;
(2)将△ABC 绕点 C 顺时针旋转 90°得到△A2B2C,画出△A2B2C,求在旋转过程中,点 A 所经过的路径长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com