
【题目】4月23日是“世界图书与版权日”(简称“世界读书日”),设立目的是推动更多的人阅读和写作,南开读书社对初三某班进行了“你最喜欢的书籍类别”的问卷调查.用“![]() ”表示小说类书籍,“
”表示小说类书籍,“![]() ”表示文学类书籍,“
”表示文学类书籍,“![]() ”表示传记类书籍,“
”表示传记类书籍,“![]() ”表示艺术类书籍.根据问卷调查统计资料绘制了如下两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
”表示艺术类书籍.根据问卷调查统计资料绘制了如下两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
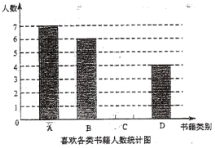
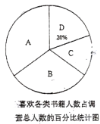
(1)本次问卷调查,共调查了 名学生,请补全下列条形统计图和扇形统计图;
(2)在接受问卷调查的学生中,喜欢“![]() ”的人中有2名是男生,喜欢“
”的人中有2名是男生,喜欢“![]() ”的人中有1名是男生,现分别从喜欢这两类书籍学生中各进行读书心得交流,请用画树状图或列表法求出刚好选中2名都是男生的概率.
”的人中有1名是男生,现分别从喜欢这两类书籍学生中各进行读书心得交流,请用画树状图或列表法求出刚好选中2名都是男生的概率.
【答案】(1)![]() 人,见解析;(2)
人,见解析;(2)![]() ,见解析
,见解析
【解析】
(1)先结合直方图中喜欢“![]() ”的人数与扇形统计图中其所占的比例求出调查总人数,再求出每一类的人数以及所占比例,补全统计图即可.
”的人数与扇形统计图中其所占的比例求出调查总人数,再求出每一类的人数以及所占比例,补全统计图即可.
(2)根据直方图中统计数据求出喜欢![]() 类和
类和![]() 类的男女生人数,再按树状图法或者列表法求解即可.
类的男女生人数,再按树状图法或者列表法求解即可.
解:(1)共接受调查的总人数为:![]() (人)
(人)
喜欢![]() 类的学生人数为:
类的学生人数为:![]() (人)
(人)
喜欢![]() 类的学生所占百分比为:
类的学生所占百分比为:![]() ,喜欢
,喜欢![]() 类的学生所占百分比为:
类的学生所占百分比为:![]() ,喜欢
,喜欢![]() 类的学生所占百分比为:
类的学生所占百分比为:![]() .
.
统计图补全如下:
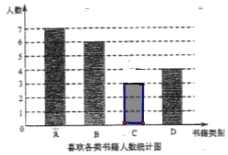
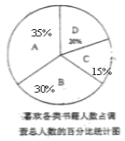
(2)通过计算可知,
喜欢![]() 类的学生是2男1女,喜欢
类的学生是2男1女,喜欢![]() 类的学生是1男3女,可作树状图如下:
类的学生是1男3女,可作树状图如下:
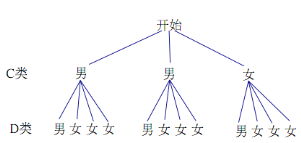
所以![]() (刚好选中2名都是男生)
(刚好选中2名都是男生)![]()
如采用列表法,则表格如下:
| 男 | 女 | 女 | 女 |
男 | (男,男) | (男,女) | (男,女) | (男,女) |
男 | (男,男) | (男,女) | (男,女) | (男,女) |
女 | (女,男) | (女,女) | (女,女) | (女,女) |
所以P(刚好选中2名都是男生)![]() (类比树状图给分)
(类比树状图给分)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
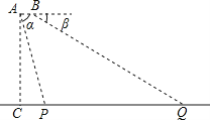
【题目】如图,为了测量一座大桥的长度,在一架水平飞行的无人机AB的尾端A点测得桥头P点的俯角α=74°,前端B点测得桥尾Q点的俯角=30°,此时无人机的飞行高度AC=868米,AB=1米.求这座大桥PQ的长度(结果保留整数)(参考数据:sin74°≈0.9,cos74°≈0.3,tan74°≈3.5,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出如下规定:对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为N上任一点,如果P,Q两点间的距离存在最小值时,就称该最小值为两个图形M和N之间的“闭距离”;如果P,Q两点间的距离存在最大值时,就称该最大值为两个图形M和N之间的“开距离”.
请你在学习,理解上述定义的基础上,解决下面问题:
在平面直角坐标系xOy中,点A(﹣6,8),B(﹣6,﹣8),C(6,﹣8),D(6,8).
(1)请在平面直角坐标系中画出四边形ABCD,线段AB和线段CD的“闭距离”为 ;“开距离”为 ;
(2)设直线y=﹣![]() x+b(b>0)与x轴,y轴分别交于点E,F,若线段EF与四边形ABCD的“闭距离”是2,求它们的“开距离”;
x+b(b>0)与x轴,y轴分别交于点E,F,若线段EF与四边形ABCD的“闭距离”是2,求它们的“开距离”;
(3)⊙M的圆心为M(m,﹣6),半径为1,若⊙M与△ABC的“闭距离”等于1,直接写出m的取值范围.
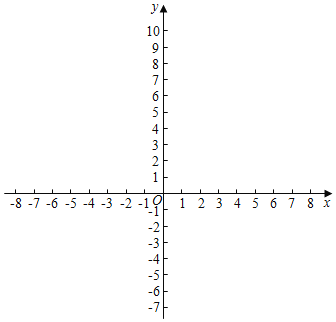
查看答案和解析>>
科目:初中数学 来源: 题型:
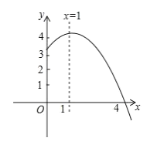
【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
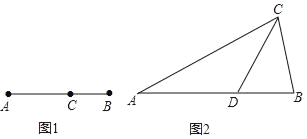
【题目】如图1,我们已经学过:点C将线段AB分成两部分,如果![]() ,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
如图2,在△ABC中,∠A=36°,AB=AC,∠C的平分线交AB于点D.
(1)证明点D是AB边上的黄金分割点;
(2)证明直线CD是△ABC的黄金分割线.
查看答案和解析>>
科目:初中数学 来源: 题型:
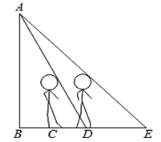
【题目】一天晚上,小颖由路灯A下的B处向正东走到C处时,测得影子CD的长为1米.当她继续向正东走到D处时,测得此时影子DE的一端E到路灯A的仰角为45°.已知小颖的身高为1.5米,那么路灯AB的高度是多少米?( )
A.4米B.4.5米C.5米D.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
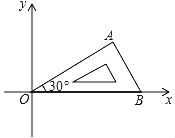
【题目】将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中,OB 在 x轴上,若 OA=2,将三角板绕原点 O 顺时针旋转 75°,则点 A 的对应点 A′ 的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
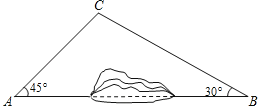
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶,已知BC=80千米,∠A=45°,∠B=30°,
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到1千米)(参考数据:![]() =1.4,
=1.4,![]() =1.7)
=1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
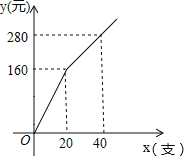
【题目】某校九年级决定购买学习用具对在本次适应性考以中成绩突出的同学进行奖励,其中计划购买,A、B两种型号的钢笔共45支,已知A种钢笔的单价为7元/支,购买B种钢笔所需费用y(元)与购买数量x(支)之间存在如图所示的函数关系式.
(1)求y与x的函数关系式;
(2)若购买计划中,B种钢笔的数最不超过35支,但不少于A种钢笔的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com