
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

【答案】(1)90°,直径所对的圆周角是直角;
(2)△EAD是等腰三角形,理由见解析;
(3)BD=![]()
【解析】试题分析:(1)根据AB是⊙O的直径,点C在⊙O上利用直径所对的圆周角是直角即可得到结论;
(2)根据∠ABC的平分线与AC相交于点D,得到∠CBD=∠ABE,再根据AE是⊙O的切线得到∠EAB=90°,从而得到∠CDB+∠CBD=90°,等量代换得到∠AED=∠EDA,从而判定△EAD是等腰三角形.
(3)证得△CDB∽△AEB后设BD=5x,则CB=4x,CD=3x,从而得到CA=CD+DA=3x+6,然后在直角三角形ACB中,利用AC2+BC2=AB2得到(3x+6)2+(4x)2=82解得x后即可求得BD的长.
试题解析:(1)∵AB是⊙O的直径,点C在⊙O上,
∴∠ACB=90°(直径所对的圆周角是直角)
(2)△EAD是等腰三角形.
证明:∵∠ABC的平分线与AC相交于点D,
∴∠CBD=∠ABE
∵AE是⊙O的切线,∴∠EAB=90°
∴∠AEB+∠EBA=90°,
∵∠EDA=∠CDB,∠CDB+∠CBD=90°,
∵∠CBE=∠ABE,
∴∠AED=∠EDA,
∴AE=AD
∴△EAD是等腰三角形.
(3)解:∵AE=AD,AD=6,
∴AE=AD=6,
∵AB=8,
∴在直角三角形AEB中,EB=10
∵∠CDB=∠E,∠CBD=∠ABE
∴△CDB∽△AEB,
∴![]() ,
,
∴设CB=4x,CD=3x则BD=5x,
∴CA=CD+DA=3x+6,
在直角三角形ACB中,
AC2+BC2=AB2
即:(3x+6)2+(4x)2=82,
解得:x=﹣2(舍去)或x=![]()
∴BD=5x=![]() .
.


科目:初中数学 来源: 题型:
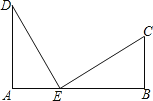
【题目】如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.(x2)3+(x3)2=2x6
B.(x2)3(x2)3=2x12
C.x4(2x)2=2x6
D.(2x)3(﹣x)2=﹣8x5
查看答案和解析>>
科目:初中数学 来源: 题型:
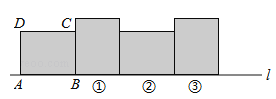
【题目】如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是( )
A. 2015π B. 3019.5π C. 3018π D. 3024π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,不能应用平方差公式进行计算的是( )
A.(-x+2y)(2y+x)B.(x+y)(x-y)C.(a-b)(-a+b)D.(-2m+n)(-2m-n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回顾学习函数的过程,由函数的表达式通过列表、描点、连线画出函数的图象,再利用函数图象研究函数的性质.这个过程中主要体现的数学方法是( )
A. 数形结合 B. 类比 C. 公理化 D. 归纳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2 > 4ac;②2a+b=0;③a-b+c=0;④5a < b.其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com