如图1，小明将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，测得AB=5，AD=4．在进行如下
操作时遇到了下面的几个问题，请你帮助解决．
（1）将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时，EF恰好经过点A（如图2），请你求出AE和FG的长度．
（2）在（1）的条件下，小明先将三角形的边EG和矩形边AB重合，然后将△EFG沿直线BC向右平移，至F点与B重合时停止．在平移过程中，设G点平移的距离为x，两纸片重叠部分
面积为y，求在平移的整个过程
中，y与x的函数关系式，并求当重叠部分面积为10时，平移距离x的值（如图3）．
（3）在（2）的操作中，小明发现在平移过程中，虽然有时平移的距离不等，但两纸片重叠的面积却是相等的；而有时候平移的距离不等，两纸片重叠部分的面积也不可能相等．请探索这两种情况下重叠部分面积y的范围（直接写出结果）．
科目：初中数学 来源： 题型：
如图，已知点P是抛物线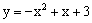
上的一动点，过点P分别作PM⊥x轴于点M，PN⊥y轴于点N，在四边形PMON上分别截取PC
=
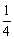MP，MD=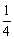OM，OE=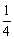ON，NF=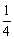NP．问：在抛物线上是否存在这样的点P，使四边形CDEF为矩形？若存在，请求出所有符合条件的P点坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，等腰梯形MNPQ的上底长为2，腰长为3，一个底角为60°．正方形ABCD的边
长为1，它的一边AD在MN上，且顶点A与M重合．现将正方形AB
CD在梯形的外面沿边MN、NP、PQ进行翻滚，翻滚到有一个顶点与Q重合即停止滚动．
求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S．
查看答案和解析>>
科目：初中数学 来源： 题型：
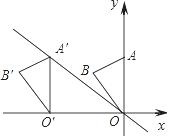
如图，在平面直角坐标系中，点A的坐标为（0，3），△OAB沿x轴向左平移后得到△O′A′B′，点A的对应点在直线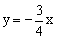
上一点，则点B与其对应点B′间的距离为【 】
A．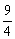
B．3 C．4 
D．5
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系中
，O为坐标原点，抛物线
与x轴相交于O、B，顶点为A，连接OA．
（1）求点A的坐标和∠AOB的度数
；
（2）若将抛物线向右平移4个单位，再向上平移2个单位，再向上翻转，得到抛物线m，其顶点为点C．连接OC和AC，把△AOC沿OA翻折得到四边形ACOC′．试判断其形状，并说明理由；
（3）在（2）的情况下，判断点C′是否在抛物线上，请说明理由；
查看答案和解析>>
科目：初中数学 来源： 题型：
操作发现
将一副直角三角板如图①摆放，能够发现等腰直角三角板A
BC的斜边与含30°角的直角三角板DEF的长直
角边DE重合．
问题解决
将图①中的等腰直角三角板ABC绕点B
顺时针旋转30°，点C落在BF上，AC与
BD交于点O，连接CD，如图②．
（1）求证：AD∥BF；
（2）若AD=2，求AB的长．
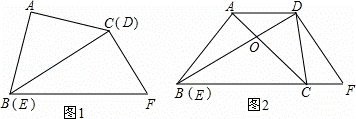
查看答案和解析>>
科目：初中数学 来源： 题型：
把所有正偶数从小到大排列，并按如下规律分组：（2，4），（6，8，10，12），（1
4，16，18，20，22，24），…，现用等式AM=（i，j）
表示正偶数M是第i组第j个数（从左往右数），如A10=（2，3），则A2014=【 】
A．（31，15） B．（31，16） 
C．（32，15） D．（32，16）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．∴
．由△BEM∽△FEB，
，∴FG=10． ..3分
；当4＜x≤10时，y=－2x+24，当y=10时，x=7或
． .6分
。