
把所有正偶数从小到大排列,并按如下规律分组:(2,4),(6,8,10,12),(1 4,16,18,20,22,24),…,现用等式AM=(i,j)
4,16,18,20,22,24),…,现用等式AM=(i,j) 表示正偶数M是第i组第j个数(从左往右数),如A10
表示正偶数M是第i组第j个数(从左往右数),如A10 =(2,3),则A2014=【 】
=(2,3),则A2014=【 】
A.(31,15) B.(31,16)  C.(32,15) D.(32,16)
C.(32,15) D.(32,16)
科目:初中数学 来源: 题型:
在平面直角坐标系中,已知抛物线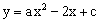 (a,c为常数)的顶点为P,
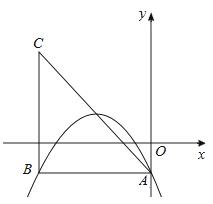
(a,c为常数)的顶点为P, 等腰直角三角形ABC的顶点A的坐标
等腰直角三角形ABC的顶点A的坐标 为(0,﹣1),C的坐标为(﹣4,3),
为(0,﹣1),C的坐标为(﹣4,3), 直角顶点B在第二象限。
直角顶点B在第二象限。
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q,若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
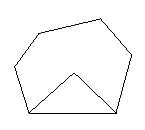
如图1,小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=5,AD=4.在进行如下 操作时遇到了下面的几个问题,请你帮助解决.
操作时遇到了下面的几个问题,请你帮助解决.




(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2),请你求出AE和FG的长度.
(2)在(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x,两纸片重叠部分 面积为y,求在平移的整个过程
面积为y,求在平移的整个过程 中,y与x的函数关系式,并求当重叠部分面积为10时,平移距离x的值(如图3).
中,y与x的函数关系式,并求当重叠部分面积为10时,平移距离x的值(如图3).
(3)在(2)的操作中,小明发现在平移过程中,虽然有时平移的距离不等,但两纸片重叠的面积却是相等的;而有时候平移的距离不等,两纸片重叠部分的面积也不可能相等.请探索这两种情况下重叠部分面积y的范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
探究与发现:
探究一:我们知道,三角形的一个外角等 于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
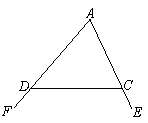
已知:如图,∠FDC与 ∠ECD
∠ECD 分别为△ADC的两个外角,
分别为△ADC的两个外角,
试探究∠A与∠FDC+∠ECD的数量关系.

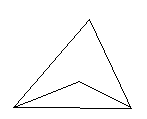
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.

探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠AD C和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
C和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.


探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠ A+∠B+∠E+∠F的数量关系: _______________________________.
A+∠B+∠E+∠F的数量关系: _______________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
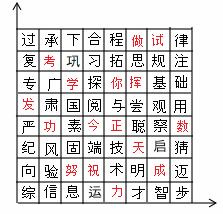
如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”。目前,已破译出“正 做数学”的真实意思是“祝你成功”。若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 。
做数学”的真实意思是“祝你成功”。若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
让我们轻松一 下,做一个数字游戏:
下,做一个数字游戏:
第一步:取一个自然数n1=5,计算n12+1得a1;
第二步:算出a1的各位数字之和得n 2,计算n22+1得a2;
2,计算n22+1得a2;
第三步:算出a2的各位数字之和得n 3,计算n32+1得a3;
3,计算n32+1得a3;
…………
依此类推,则a2008=___ __.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,n个边长为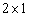 的相邻矩形的一边均在同一直线上,点M1,M2,M3,……Mn分别为边B1B2,B2B3,B3B4,……,BnBn+1的中点,△B1C1M
的相邻矩形的一边均在同一直线上,点M1,M2,M3,……Mn分别为边B1B2,B2B3,B3B4,……,BnBn+1的中点,△B1C1M 1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn
1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn 的面积为Sn,则Sn= 。(用含n的式子表示)
的面积为Sn,则Sn= 。(用含n的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com