
探究与发现:
探究一:我们知道,三角形的一个外角等 于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
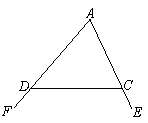
已知:如图,∠FDC与 ∠ECD
∠ECD 分别为△ADC的两个外角,
分别为△ADC的两个外角,
试探究∠A与∠FDC+∠ECD的数量关系.

探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
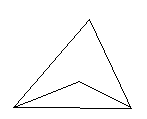
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.

探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠AD C和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
C和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.


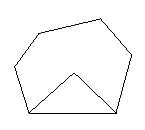
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠ A+∠B+∠E+∠F的数量关系: _______________________________.
A+∠B+∠E+∠F的数量关系: _______________________________.

科目:初中数学 来源: 题型:
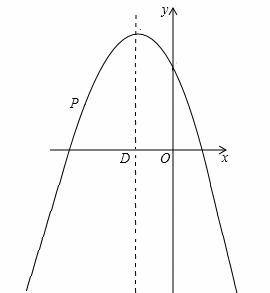
如图,在平面直角坐标系xOy中,点P(x,y)是抛物线 上的一个动点,抛物线的对称轴与x轴交于点D,经过点P的直线PE与y轴交于点E,是否存在△OPE与△OPD全等?若存在,请求出直线PE的解析式;若不存在,请说明理由。
上的一个动点,抛物线的对称轴与x轴交于点D,经过点P的直线PE与y轴交于点E,是否存在△OPE与△OPD全等?若存在,请求出直线PE的解析式;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边 长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形AB
长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形AB CD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.
CD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.


求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中 ,O为坐标原点,抛物线
,O为坐标原点,抛物线 与x轴相交于O、B,顶点为A,连接OA.
与x轴相交于O、B,顶点为A,连接OA.
(1)求点A的坐标和∠AOB的度数 ;
;
(2)若将抛物线 向右平移4个单位,再向上平移2个单位,再向上翻转,得到抛物线m,
向右平移4个单位,再向上平移2个单位,再向上翻转,得到抛物线m, 其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
(3)在(2)的情况下,判断点C′是否在抛物线 上,请说明理由;
上,请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
操作发现
将一副直角三角板如图①摆放,能够发现等腰直角三角板A BC的斜边与含30°角的直角三角板DEF的长直
BC的斜边与含30°角的直角三角板DEF的长直 角边DE重合.
角边DE重合.
问题解决
 将图①中的等腰直角三角板ABC绕点B
将图①中的等腰直角三角板ABC绕点B 顺时针旋转30°,点C落在BF上,AC与
顺时针旋转30°,点C落在BF上,AC与 BD交于点O,连接CD,如图②.
BD交于点O,连接CD,如图②.
(1)求证:AD∥BF;
(2)若AD=2,求AB的长.
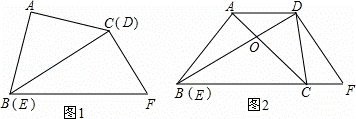
查看答案和解析>>
科目:初中数学 来源: 题型:
我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不 与点A,B重合),D是半圆
与点A,B重合),D是半圆
 的中点,C,D在直径AB
的中点,C,D在直径AB 的两侧,若在⊙O内存在点E,
的两侧,若在⊙O内存在点E, 使AE=AD,CB=CE.
使AE=AD,CB=CE.
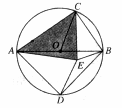

①求证:△ACE是奇异三角形;
②当△A CE是直角三角形时,求∠AOC的度数.
CE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
把所有正偶数从小到大排列,并按如下规律分组:(2,4),(6,8,10,12),(1 4,16,18,20,22,24),…,现用等式AM=(i,j)
4,16,18,20,22,24),…,现用等式AM=(i,j) 表示正偶数M是第i组第j个数(从左往右数),如A10
表示正偶数M是第i组第j个数(从左往右数),如A10 =(2,3),则A2014=【 】
=(2,3),则A2014=【 】
A.(31,15) B.(31,16)  C.(32,15) D.(32,16)
C.(32,15) D.(32,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
一个盒子里有完全相同的三个小球,球上分别标有数字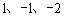 。随机摸
。随机摸 出一个小球(不放回)其数字记为p ,再随机摸出另一个小球其数字记为q ,则
出一个小球(不放回)其数字记为p ,再随机摸出另一个小球其数字记为q ,则 满足关于的方程
满足关于的方程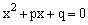 有实数
有实数 根的概率是【 】
根的概率是【 】
A.  B.
B. 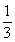
 C.
C. 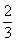 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com