【题目】如图，已知E是平行四边形ABCD中DA边的延长线上一点，且AD＝2AE，连接EC分别交AB，BD于点F，G．
（1）求证：BF＝2AF；
（2）若BD＝20cm，求DG的长．
【答案】（1）证明见解析；（2）12cm．
【解析】
（1）根据平行四边形的性质得到AB∥CD，AD∥BC，利用平行线分线段成比例定理进行分析从而得到结论；
（2）根据平行四边形的性质AB=CD，则利用BF=2AF得到BF＝
AB＝CD，再利用BF∥CD，根据平行线分线段成比例定理得到
＝
＝，然后根据比例的性质求DG的长．
解：（1）∵四边形ABCD为平行四边形，
∴AB∥CD，AD∥BC，
∵AF∥CD，
∴
＝
＝
，
∵AE∥BC，
∴
＝＝，
∴BF＝2AF；
（2）解：∵四边形ABCD为平行四边形，
∴AB＝CD，
而BF＝2AF，
∴BF＝AB＝CD，
∵BF∥CD，
∴＝＝，
∴
＝
，
∴DG＝
BD＝×20＝12cm．
科目：初中数学 来源： 题型：
【题目】某旅游团到永定土楼观光，计划购买A型、B型两种型号的土楼模型．若购买8个A型土楼模型和5个B型土楼模型需用1540元；若购买4个A型土楼模型和6个B型土楼模型需用1120元．求A，B两种型号土楼模型的单价分别是多少元．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在半圆
中，直径
的长为6，点
是半圆上一点，过圆心作的垂线交线段
的延长线于点
，交弦
于点
．
（1）求证：
；
（2）记
，
，求
关于
的函数表达式；
（3）若
，求图中阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，∠C=90°，AD⊥DB，点E为AB的中点，DE∥BC．
（1）求证：BD平分∠ABC；
（2）连接EC，若∠A=30°，DC
，求EC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
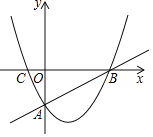
【题目】如图，直线y＝
x﹣2与x轴交于点B，与y轴交于点A，抛物线y＝ax2﹣
x+c经过A，B两点，与x轴的另一交点为C．
（1）求抛物线的解析式；
（2）M为抛物线上一点，直线AM与x轴交于点N，当
时，求点M的坐标；
（3）P为抛物线上的动点，连接AP，当∠PAB与△AOB的一个内角相等时，直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列图形：
（1）可知tanα＝
，tanβ＝
，用“画图法”求tan（α+β）的值，具体解法如下：
第一步：如图1所示，构造符合题意两个“背靠背”的直角三角形；
第二步：如图2所示，将图1中所有数据同比例扩大3倍；
第三步：如图3所示，依托中间的Rt△ABD的各顶点构造“水平﹣﹣竖直辅助线”，构造出“一线三直角”基本相似型，并补成矩形ACEF；由图可知tan（α+β）＝ ．
（2）依据（1）的方法，已知tanα＝，tanβ＝
，用“画图法”求tan（α+β）的值．
（3）扩展延伸，已知tanα＝，tanβ＝，直接写出tan（α﹣β）＝ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，将矩形ABCD折叠，使点C与点A重合，点D落在点G处，折痕为EF．
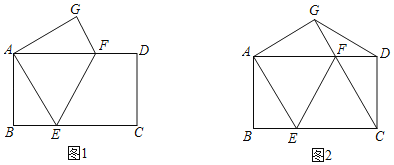
（1）如图1，求证：BE＝GF；
（2）如图2，连接CF、DG，若CE＝2BE，在不添加任何辅助线的情况下，请直接写出图2中的四个三角形，使写出的每个三角形都为等腰三角形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某初中学校举行校园歌唱大赛，对各年级同学的获奖情况进行了统计，并绘制了如下两幅不完整的统计图，请结合图中相关数据解答下列题：
（1）请将条形统计图补全；
（2）获得一等奖的同学中有
来自七年级，有来自八年级，其他同学均来自九年级，现准备从获得一等奖的同学中任选两人参加全市校园歌唱大赛，请通过列表或画树状图求所选出的两人中有七年级或八年级同学的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
