
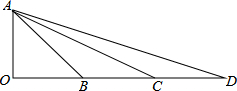
 如图,∠AOD=90°,OA=OB=BC=CD,∠BAC=20°,求∠D的度数.
如图,∠AOD=90°,OA=OB=BC=CD,∠BAC=20°,求∠D的度数.| 2 |
| a2+(2a)2 |
| 5 |
| a2+(3a)2 |
| 10 |
| AD |
| AC |
| ||
|
| 2 |
| BD |
| AB |
| 2a | ||
|
| 2 |
| AB |
| BC |
| ||
| a |
| 2 |
| AD |
| AC |
| BD |
| AB |
| AB |
| BC |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
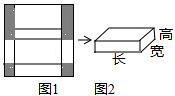 七年级(5)班开展“我的中国梦“主题班会活动,需要制作一个“梦之盒”,用来装同学们的卡片,图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是多少cm3?
七年级(5)班开展“我的中国梦“主题班会活动,需要制作一个“梦之盒”,用来装同学们的卡片,图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是多少cm3?查看答案和解析>>
科目:初中数学 来源: 题型:
| 19 |
| 32 |
| 57 |
| 64 |
| 85 |
| 128 |
查看答案和解析>>
科目:初中数学 来源: 题型:
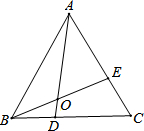 如图,点D,E分别在等边△ABC的BC,CA边上,连接AD,BE相交于点O,且∠BOD=60°.
如图,点D,E分别在等边△ABC的BC,CA边上,连接AD,BE相交于点O,且∠BOD=60°.查看答案和解析>>
科目:初中数学 来源: 题型:
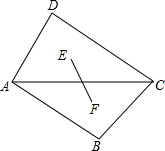 将两块三角尺按如图方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=12,点E,F分别是△ACD,△ABC的重心,求EF的长.
将两块三角尺按如图方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=12,点E,F分别是△ACD,△ABC的重心,求EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、-1 | B、-1-i |
| C、-1+i | D、i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com