
【题目】一个有进水管与出水管的容器,从某时刻开始的![]() 内只进水不出水,在随后的
内只进水不出水,在随后的![]() 内既进水又出水,每分钟进水量和出水量是两个常数.容器内的水量
内既进水又出水,每分钟进水量和出水量是两个常数.容器内的水量![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:
(单位:![]() )之间的关系如图所示.
)之间的关系如图所示.
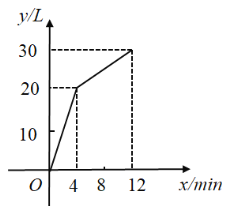
(1)当![]() 时,求出
时,求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)每分钟的进水量与出水量各是多少?
科目:初中数学 来源: 题型:
【题目】某校在参加了全市教育质量综合评价学业素养测试后,随机抽取八年级部分学生,针对发展水平四个维度“阅读素养、数学素养、科学素养、人文素养”,开展了“你最需要提升的学业素养”问卷调查(每名学生必选且只能选择一项).小明、小颖和小雯在协助老师进行统计后,有这样一段对话:
小明:“选科学素养和人文素养的同学分别为![]() 人,
人,![]() 人.”
人.”
小颖:“选数学素养的同学比选阅读素养的同学少![]() 人.”
人.”
小雯:“选科学素养的同学占样本总数的![]() .”
.”
(1)这次抽样调查了多少名学生?
(2)样本总数中,选“阅读素养”、“数学素养”的学生各多少人?
(3)如图是调查结果整理后绘制成的扇形图.请直接在横线上补全相关百分比,并求出“数学素养”所对应的圆心角度数;
(4)该校八年级有学生![]() 人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?
人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?
[Failed to download image : blob:http://qbm.xkw.com/61c6a1d7-da76-4939-b41e-e8015f4fdd80]
查看答案和解析>>
科目:初中数学 来源: 题型:
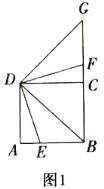
【题目】(1)如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .写出线段
.写出线段![]() ,
,![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
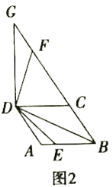
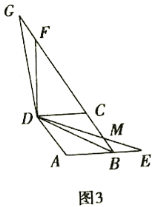
(2)当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() 、
、![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①如图2,点![]() 在线段
在线段![]() 上时,请探究线段
上时,请探究线段![]() ,
,![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是弧AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P作PN⊥MB于点N.已知AB =6cm,设A 、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P与点A或点B重合时,y的值为0)
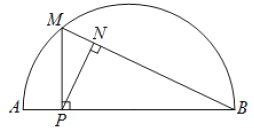
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.0 | 2.3 | 2.1 | 0.9 | 0 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 轴上的点,且
轴上的点,且![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 轴正半轴上的任意一点,连结
轴正半轴上的任意一点,连结![]() ,以
,以![]() 为边按顺时针方向作正方形
为边按顺时针方向作正方形![]() .
.

(1)填空:点![]() 的坐标为______;
的坐标为______;
(2)记正方形![]() 的面积为
的面积为![]() ,①求
,①求![]() 关于
关于![]() 的函数关系式;②当
的函数关系式;②当![]() 时,求
时,求![]() 的值.
的值.
(3)是否存在满足条件的![]() 的值,使正方形的顶点
的值,使正方形的顶点![]() 或
或![]() 落在
落在的边上?若存在,求出所有满足条件的
![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
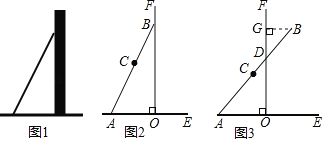
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
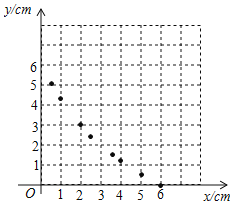
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l及直线l外一点P.如图,
(1)在直线l上取一点A,连接PA;
(2)作PA的垂直平分线MN,分别交直线l,PA于点B,O;
(3)以O为圆心,OB长为半径画弧,交直线MN于另一点Q;
(4)作直线PQ.
根据以上作图过程及所作图形,下列结论中错误的是( )
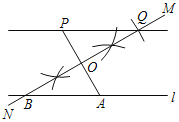
A.△OPQ≌△OABB.PQ∥AB
C.AP=![]() BQD.若PQ=PA,则∠APQ=60°
BQD.若PQ=PA,则∠APQ=60°
查看答案和解析>>
科目:初中数学 来源: 题型:
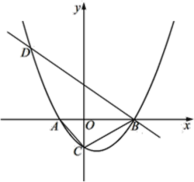
【题目】如图,已知抛物线![]() (
(![]() 为常数,且
为常数,且![]() )与
)与![]() 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与![]() 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线![]() 与抛物线的另一交点为D,点D的横坐标为-4.
与抛物线的另一交点为D,点D的横坐标为-4.
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)求抛物线的函数解析式;
(3)分别求出tan∠ABC和tan∠BAC的值;
(4)在第一象限的抛物线上是否存在点P,使得以A,B,P为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com