
【题目】已知直线l及直线l外一点P.如图,
(1)在直线l上取一点A,连接PA;
(2)作PA的垂直平分线MN,分别交直线l,PA于点B,O;
(3)以O为圆心,OB长为半径画弧,交直线MN于另一点Q;
(4)作直线PQ.
根据以上作图过程及所作图形,下列结论中错误的是( )
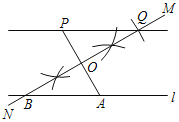
A.△OPQ≌△OABB.PQ∥AB
C.AP=![]() BQD.若PQ=PA,则∠APQ=60°
BQD.若PQ=PA,则∠APQ=60°
【答案】C
【解析】
连接AQ,BP,如图,利用基本作图得到BQ垂直平分PA,OB=OQ,则可根据“SAS”判断△OAB≌△OPQ,根据全等三角形的性质得∠ABO=∠PQO,于是可判断PQ∥AB;由BQ垂直平分PA得到QP=QA,若PQ=PA,则可判断△PAQ为等边三角形,于是得到∠APQ=60°,从而可对各选项进行判断.
解:连接AQ,BP,如图,
由作法得BQ垂直平分PA,OB=OQ,
∴∠POQ=∠AOB=90°,OP=OA,
∴△OAB≌△OPQ(SAS);
∴∠ABO=∠PQO,
∴PQ∥AB;
∵BQ垂直平分PA,
∴QP=QA,
若PQ=PA,则PQ=QA=PA,此时△PAQ为等边三角形,则∠APQ=60°.
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
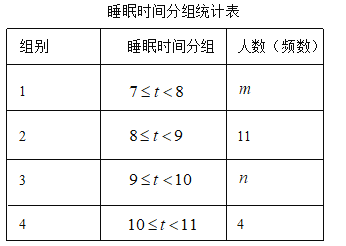
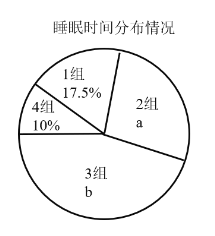
【题目】为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了部分学生,调查了他们平均每天的睡眠时间(单位:![]() ).以下是根据调查结果绘制的统计图表的一部分.
).以下是根据调查结果绘制的统计图表的一部分.
请根据以上信息,解答下列问题:
(1)共随机抽取_______名学生;
(2)![]() _____,
_____,![]() _______,
_______,![]() ______,
______,![]() ______;
______;
(3)抽取的这40名学生平均每天睡眠时间的中位数落在______组(填组别);
(4)如果按照学校要求,学生平均每天的睡眠时间应不少于![]() ,请估计该校学生中睡眠时间符合要求的人数.
,请估计该校学生中睡眠时间符合要求的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管与出水管的容器,从某时刻开始的![]() 内只进水不出水,在随后的
内只进水不出水,在随后的![]() 内既进水又出水,每分钟进水量和出水量是两个常数.容器内的水量
内既进水又出水,每分钟进水量和出水量是两个常数.容器内的水量![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:
(单位:![]() )之间的关系如图所示.
)之间的关系如图所示.
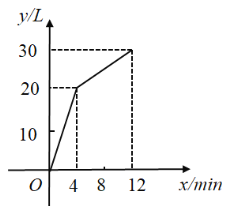
(1)当![]() 时,求出
时,求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)每分钟的进水量与出水量各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.
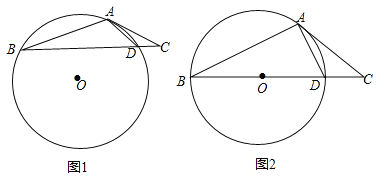
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() 的顶点
的顶点![]() 均在格点上.
均在格点上.
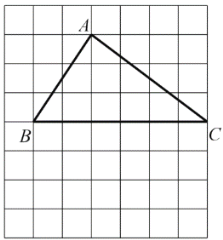
(Ⅰ)![]() 的长等于__________;
的长等于__________;
(Ⅱ)请用无刻度的直尺,在如图所示的网格中,画出点![]() ,点E在
,点E在![]() 上,且
上,且![]() ,点F在
,点F在![]() 上,使其满足
上,使其满足![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目:初中数学 来源: 题型:
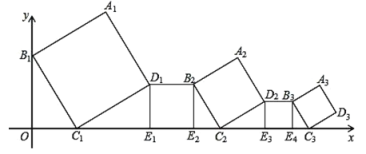
【题目】一组正方形按如图所示放置,其中顶点 B1 在 y 轴上,顶点 C1,E1,E2,C2,E3,E4,C3… 在 x 轴上.已知正方形 A1B1C1D1 的边长为 1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则正方形 A2020B2020C2020D2020 的边长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 直线
直线![]() 经过点
经过点![]() .
.
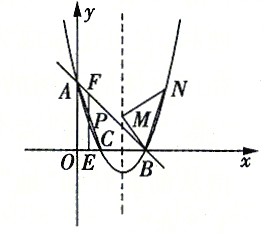
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方的抛物线上一动点,过点
下方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 设点
设点![]() 的横坐标为
的横坐标为![]() 若
若![]() 求
求![]() 的值;
的值;
(3)![]() 是第一象限对称轴右侧抛物线上的一点,连接
是第一象限对称轴右侧抛物线上的一点,连接![]() 抛物线的对称轴上是否存在点
抛物线的对称轴上是否存在点![]() .使得
.使得![]() 与
与![]() 相似,且
相似,且![]() 为直角,若存在,请直接写出点
为直角,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课程:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查的结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
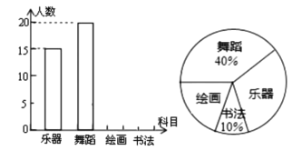
(1)本次共调查了多少名学生?
(2)请将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名男同学,其余为女同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请你用列表或画树状图的方法,求所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com