
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 轴上的点,且
轴上的点,且![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 轴正半轴上的任意一点,连结
轴正半轴上的任意一点,连结![]() ,以
,以![]() 为边按顺时针方向作正方形
为边按顺时针方向作正方形![]() .
.

(1)填空:点![]() 的坐标为______;
的坐标为______;
(2)记正方形![]() 的面积为
的面积为![]() ,①求
,①求![]() 关于
关于![]() 的函数关系式;②当
的函数关系式;②当![]() 时,求
时,求![]() 的值.
的值.
(3)是否存在满足条件的![]() 的值,使正方形的顶点
的值,使正方形的顶点![]() 或
或![]() 落在
落在的边上?若存在,求出所有满足条件的
![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() .(2)①
.(2)①![]() .②
.②![]() .(3)
.(3)![]() ,21,3,
,21,3,![]() .
.
【解析】
(1)根据点C的坐标和正弦的定义即可求出AC,利用勾股定理即可求出OA,从而求出结论;
(2)①过点![]() 作
作![]() 轴于点
轴于点![]() ,易证DH为
,易证DH为![]() 的中位线,根据三角形中位线的性质可得
的中位线,根据三角形中位线的性质可得![]() ,
,![]() ,
,![]() ,然后根据正方形的面积公式和勾股定理即可求出结论;
,然后根据正方形的面积公式和勾股定理即可求出结论;
②易知此时点![]() 即为正方形
即为正方形![]() 的中心,从而得出
的中心,从而得出![]() ,从而求出a的值,结合①的结论即可求出S;
,从而求出a的值,结合①的结论即可求出S;
(3)根据点F和点G落在![]() 的各边分类讨论,分别画出对应的图形,根据全等三角形的判定及性质、相似三角形的判定及性质即可分别求出结论.
的各边分类讨论,分别画出对应的图形,根据全等三角形的判定及性质、相似三角形的判定及性质即可分别求出结论.
解:(1)∵![]() ,
,![]()
∴OC=8,![]()
解得:AC=10
根据勾股定理可得OA=![]()
∵点A在x轴负半轴上
∴![]()
故答案为:![]() .
.
(2)①如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
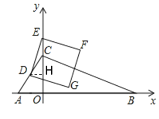
∵![]() 为线段
为线段![]() 的中点,DH⊥y轴,AO⊥y轴
的中点,DH⊥y轴,AO⊥y轴
∴DH∥AO
∴DH为![]() 的中位线
的中位线
∴![]() ,
,![]()
∴![]() ,
,
∴![]() .
.
②当![]() 时,点
时,点![]() 即为正方形
即为正方形![]() 的中心,
的中心,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)①当点![]() 落在
落在![]() 边上时,如图,过点D作DM⊥y轴于M,过点F作FN⊥y轴于N
边上时,如图,过点D作DM⊥y轴于M,过点F作FN⊥y轴于N
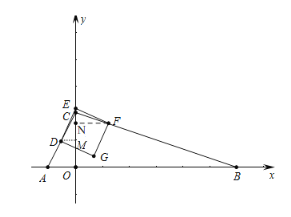
∴∠EMD=∠FNE=90°
∵四边形DGFE为正方形
∴ED=FE,∠DEF=90°
∴∠DEM+∠FEN=90°,∠EFN+∠FEN=90°
∴∠DEM=∠EFN
∴![]() ≌
≌![]()
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵FN平行OB
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
②当点![]() 落在
落在![]() 边上时,如图,过点D作DM⊥y轴于M,过点G作GQ⊥x轴于Q,QG的延长线于DM的延长线交于点N
边上时,如图,过点D作DM⊥y轴于M,过点G作GQ⊥x轴于Q,QG的延长线于DM的延长线交于点N

∴∠EMD=∠DNG=90°
∵四边形DGFE为正方形
∴ED=DG,∠EDG=90°
∴∠DEM+∠EDN=90°,∠GDN+∠EDN =90°
∴∠DEM=∠GDN
∴![]() ≌
≌![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴tanB=![]()
∴![]()
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
③当点![]() 落在
落在![]() 边上时,如图,过点D作DM⊥y轴于点M
边上时,如图,过点D作DM⊥y轴于点M
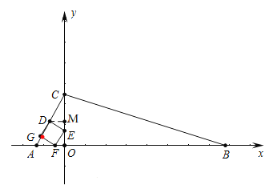
∴∠EMD=∠FOE=90°
∵四边形DGFE为正方形
∴ED=FE,∠DEF=90°
∴∠DEM+∠FEO=90°,∠EFO+∠FEO=90°
∴∠DEM=∠EFO
∴![]() ≌
≌![]()
∴![]() ,即
,即![]() .
.
④当点![]() 落在
落在![]() 边上时,如图,
边上时,如图,
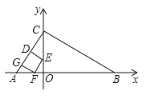
∵∠CDE=∠COA=90°,∠DCE=∠OCA
∴![]() ∽
∽![]()
∴![]() ,
,
∴![]() ,
,
得![]() .
.
综上,所有满足条件的![]() 的值有四个:
的值有四个:![]() ,21,3,
,21,3,![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点
轴交点![]() ,抛物线
,抛物线![]() 过
过![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
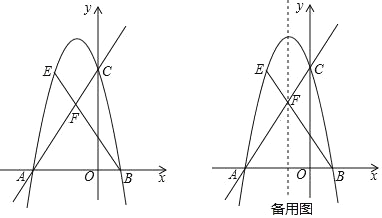
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)在直线![]() 上方的抛物线上是否存在点
上方的抛物线上是否存在点![]() ,使
,使![]() 与
与![]() 的交点
的交点![]() 恰好为
恰好为![]() 的中点?如果存在,求出点
的中点?如果存在,求出点![]() 的坐标,如果不存在,说明理由.
的坐标,如果不存在,说明理由.
(3)若点![]() 在抛物线上且横坐标为
在抛物线上且横坐标为![]() ,点
,点![]() 是抛物线对称轴上一点,在抛物线上存在一点
是抛物线对称轴上一点,在抛物线上存在一点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?直接写出点
为顶点的四边形是平行四边形?直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,给出了格点四边形ABCD(顶点为网格线的交点).
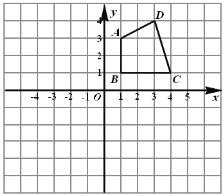
(1)画出四边形ABCD关于x轴成轴对称的四边形A1B1C1D1;
(2)以O为位似中心,在第三象限画出四边形ABCD的位似四边形A2B2C2D2,且位似比为1;
(3)在第一象限内找出格点P,使∠DCP=∠CDP,并写出点P的坐标(写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管与出水管的容器,从某时刻开始的![]() 内只进水不出水,在随后的
内只进水不出水,在随后的![]() 内既进水又出水,每分钟进水量和出水量是两个常数.容器内的水量
内既进水又出水,每分钟进水量和出水量是两个常数.容器内的水量![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:
(单位:![]() )之间的关系如图所示.
)之间的关系如图所示.
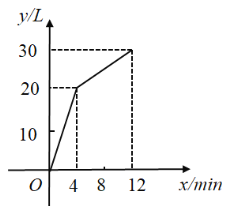
(1)当![]() 时,求出
时,求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)每分钟的进水量与出水量各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯![]() 长为
长为![]() ,坡角
,坡角![]() 为
为![]() ”改造后的斜坡式自动扶梯的坡角
”改造后的斜坡式自动扶梯的坡角![]() 为
为![]() ,若国标规定自动扶梯的速度一般是
,若国标规定自动扶梯的速度一般是![]() ,请你计算乘坐改造后的斜坡式自动扶梯比乘坐阶梯式自动扶梯多用的时间.(结果保留整数,参考数据:
,请你计算乘坐改造后的斜坡式自动扶梯比乘坐阶梯式自动扶梯多用的时间.(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() .)
.)
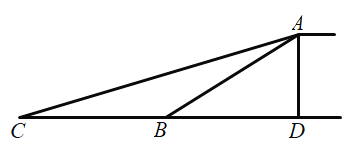
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.
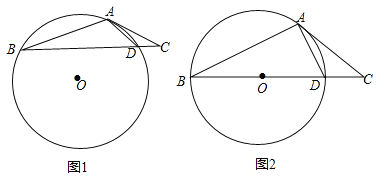
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示放置,其中顶点 B1 在 y 轴上,顶点 C1,E1,E2,C2,E3,E4,C3… 在 x 轴上.已知正方形 A1B1C1D1 的边长为 1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则正方形 A2020B2020C2020D2020 的边长是______.
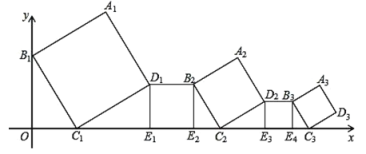
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读材料,再解答问题:
已知点![]() 和直线
和直线![]() ,则点
,则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.例如:求点
计算.例如:求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线![]() 可知:
可知:![]() .
.
所以点![]() 到直线
到直线![]() 的距离为
的距离为![]()
![]() .
.
求:(1)已知直线![]() 与
与![]() 平行,求这两条平行线之间的距离;
平行,求这两条平行线之间的距离;
(2)已知直线![]() 分别交
分别交![]() 轴于
轴于![]() 两点,
两点,![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,![]() 为
为![]() 上的动点,试求
上的动点,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com