
【题目】如图1,在 ![]() 中,以
中,以 ![]() 为直径的⊙O,交
为直径的⊙O,交 ![]() 于点
于点 ![]() ,且
,且 ![]() ,交线段
,交线段 ![]() 的延长线于点
的延长线于点 ![]() ,连接
,连接 ![]() ,过点
,过点 ![]() 作
作 ![]() 于点
于点 ![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)在 ![]() 的内部作
的内部作 ![]() ,使
,使 ![]() ,
, ![]() 分别交于
分别交于 ![]() 、
、 ![]() 于点
于点 ![]() 、
、 ![]() ,交⊙O于点
,交⊙O于点 ![]() ,若
,若 ![]() ,求
,求 ![]() 的长.
的长.
【答案】(Ⅰ)证明:过点C作CH⊥BA 交BA的延长线于H,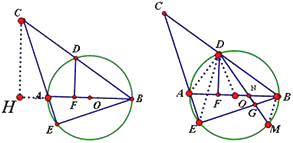
∵ ![]() ,
, ![]() ,
,
∴DF为![]() BHC的中位线,CH=2DF,
BHC的中位线,CH=2DF,
连接AD,
∵AB是直径,
∴∠ADB=90°,
又∵BD=CD,
∴![]() ABC是等腰三角形∴AB=AC,
ABC是等腰三角形∴AB=AC,
∵∠AEB =90°=∠AHC ,∠BAE =∠CAH
∴![]() AEB≌
AEB≌![]() AHC
AHC
∴CH=BE , ![]()
(Ⅱ)解:连接DA、DO、DE、BM,
∴∠ADE=∠ABE=∠BDM
∵ ![]() , BN=
, BN= ![]() ,
,
∴由(Ⅰ)可知, BE=2DF= ![]() ,
,
∵⊿CEB为直角三角形, BD=CD,
∴DE=DB , 又∠ADE=∠BDN ∠AED=∠DBN
∴![]() ADE≌
ADE≌![]() NDB
NDB
∴AD=DN BN=AE= ![]()
∵AB是直径,
∴∠ADB=∠AEB =90° BE=2DF= ![]() , AE=
, AE= ![]() . AB=3
. AB=3 ![]()
∵ ![]() AD=DN ∴ FN=AF=
AD=DN ∴ FN=AF= ![]() . DF=
. DF= ![]() ∴DN=3
∴DN=3 ![]()
在![]() ADN与
ADN与![]() BMN中,可证
BMN中,可证![]() ADN∽
ADN∽![]() MBN,得出AN
MBN,得出AN![]() NB=MN
NB=MN![]() DN
DN
∴MN=2 ![]()
在![]() DBG与
DBG与![]() DMB中,
DMB中,
∵DC=DE=DB
∴∠DMB=∠DBE=∠DEB, ∠BDG=∠BDM,
可证![]() DBG∽
DBG∽![]() DMB,
DMB,
得出DB2=DG×DM ![]() ,FB=2
,FB=2 ![]()
∴DB=6, DM=DN+MN=3 ![]() +2
+2 ![]() =5
=5 ![]()
∴36=DG×5 ![]() , DG=
, DG= ![]() ,
,
∴ MG= ![]() .
.
【解析】本题考查全等三角形的判定与性质、相似三角形的判定与性质,注意分析题目中条件,找足![]() AEB和
AEB和![]() AHC全等、
AHC全等、![]() ADE和
ADE和![]() NDB全等,和
NDB全等,和![]() ADN∽
ADN∽![]() MBN、
MBN、![]() DBG∽
DBG∽![]() DMB的条件,推导求解.
DMB的条件,推导求解.
【考点精析】掌握三角形中位线定理和相似三角形的判定与性质是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示. 
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500.
(1)设李明每月获得利润为w(元),求出w与x的函数关系式.
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)当销售单价定为多少元时,每月可获得最大利润?得最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的半径OA=4,P是OA延长线上一点,线段OP的垂直平分线分别交OP、半圆O于B、C两点,射线PC交半圆O于点D.设PA=x,CD=y,则能表示y与x的函数关系的图象是( )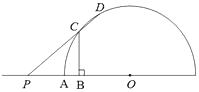
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+1的图象与反比例函数y2= ![]() 的图象交与A(1,M),B(n,﹣1)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO,BO.得出以下结论:
的图象交与A(1,M),B(n,﹣1)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO,BO.得出以下结论:
①点A和点B关于直线y=﹣x对称;
②当x<1时,y2>y1;
③S△AOC=S△BOD;
④当x>0时,y1 , y2都随x的增大而增大.
其中正确的是( )
A.①②③
B.②③
C.①③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,抛物线l1:y=ax2﹣4ax+5+4a(a<0)的顶点为A,直线l2:y=kx+3过点A,直线l2与抛物线l1及y轴分别交于B,C.
(1)求k的值;
(2)若B为AC的中点,求a的值;
(3)在(2)的条件下,直接写出不等式ax2﹣4ax+5+4a<kx+3的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2﹣2 ![]() ax﹣9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
ax﹣9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时, ![]() +
+ ![]() 均为定值,并求出该定值.
均为定值,并求出该定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() 与y轴交于点A,与直线y=﹣
与y轴交于点A,与直线y=﹣ ![]() 交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣
交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣ ![]() 上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A.﹣2 ![]()
B.﹣2≤h≤1
C.﹣1 ![]()
D.﹣1 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com