
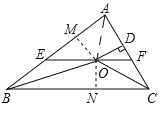
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() 下列结论:①
下列结论:①![]() ;②点
;②点![]() 到
到![]() 各边的距离相等;③
各边的距离相等;③![]() ;④设
;④设![]() ,
,![]() ,则
,则![]() ;⑤
;⑤![]() .其中正确的结论是.__________.
.其中正确的结论是.__________.

【答案】①②③⑤
【解析】
由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得③∠BOC=90°+![]() ∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD=m,AE+AF=n,则S△AEF=
∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD=m,AE+AF=n,则S△AEF=![]() mn,故④错误,根据HL证明△AMO≌△ADO得到AM=AD,同理可证BM=BN,CD=CN,变形即可得到⑤正确.
mn,故④错误,根据HL证明△AMO≌△ADO得到AM=AD,同理可证BM=BN,CD=CN,变形即可得到⑤正确.
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣
∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣![]() ∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+
∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+![]() ∠A;故③正确;
∠A;故③正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF.
∵EF∥BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA.
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=![]() AEOM+
AEOM+![]() AFOD=
AFOD=![]() OD(AE+AF)=
OD(AE+AF)=![]() mn;故④错误;
mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到△ABC各边的距离相等,故②正确;
∵AO=AO,MO=DO,∴△AMO≌△ADO(HL),∴AM=AD;
同理可证:BM=BN,CD=CN.
∵AM+BM=AB,AD+CD=AC,BN+CN=BC,∴AD=![]() (AB+AC﹣BC)故⑤正确.
(AB+AC﹣BC)故⑤正确.
故答案为:①②③⑤.


科目:初中数学 来源: 题型:
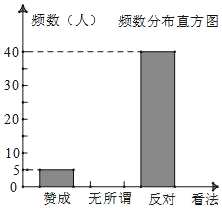
【题目】校园手机现象已经受到社会的广泛关注.某校的一个兴趣小组对“是否赞成中学生带手机进校园”的问题在该校校园内进行了随机调查.并将调查数据作出如下不完整的整理;
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |
(1)本次调查共调查了 人;(直接填空)
(2)请把整理的不完整图表补充完整;
(3)若该校有3000名学生,请您估计该校持“反对”态度的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
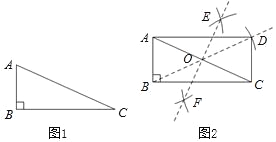
【题目】下面是“利用直角三角形作矩形”尺规作图的过程.
已知:如图1,在Rt△ABC中,∠ABC=90°.
求作:矩形ABCD.
小明的作法如下:
如图2,(1)分别以点A、C为圆心,大于![]() AC同样长为半径作弧,两弧交于点E、F;
AC同样长为半径作弧,两弧交于点E、F;
(2)作直线EF,直线EF交AC于点O;
(3)作射线BO,在BO上截取OD,使得OD=OB;
(4)连接AD,CD.
∴四边形ABCD就是所求作的矩形.
老师说,“小明的作法正确.”
请回答,小明作图的依据是:__________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
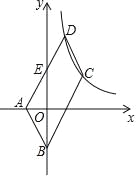
【题目】如图,平行四边形 ABCD 中,A(﹣1,0)、B(0,﹣2),顶点 C、D 在双曲线 y= (x>0)上,边 AD 交 y 轴于点 E,若点 E 恰好是 AD 的中点,则 k=_____.
(x>0)上,边 AD 交 y 轴于点 E,若点 E 恰好是 AD 的中点,则 k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC≌Rt△CED,点B、C、E在同一直线上,则结论:①AC=CD,②AC⊥CD,③BE=AB+DE,④AB∥ED,其中成立的有( )

A. 仅① B. 仅①③ C. 仅①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com