
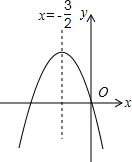
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0;其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0;其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 首先根据二次函数y=ax2+bx+c的图象经过原点,可得c=0,所以abc=0;然后根据x=1时,y<0,可得a+b+c<0;再根据图象开口向下,可得a<0,图象的对称轴为x=-$\frac{3}{2}$,可得-$\frac{b}{2a}=-\frac{3}{2}$,b<0,所以b=3a,a>b;最后根据二次函数y=ax2+bx+c图象与x轴有两个交点,可得△>0,所以b2-4ac>0,4ac-b2<0,据此解答即可.
解答 解:∵二次函数y=ax2+bx+c图象经过原点,
∴c=0,
∴abc=0
∴①正确;
∵x=1时,y<0,
∴a+b+c<0,
∴②不正确;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴是x=-$\frac{3}{2}$,
∴-$\frac{b}{2a}=-\frac{3}{2}$,b<0,
∴b=3a,
又∵a<0,b<0,
∴a>b,
∴③正确;
∵二次函数y=ax2+bx+c图象与x轴有两个交点,
∴△>0,
∴b2-4ac>0,4ac-b2<0,
∴④正确;
综上,可得
正确结论有3个:①③④.
故选:C.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:选择题
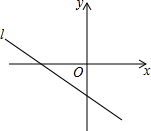 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )| A. | 1<a<2 | B. | -2<a<0 | C. | -3≤a≤-2 | D. | -10<a<-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
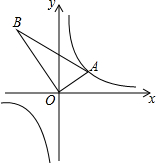 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=a2-b2 | B. | 3ab-ab=2ab | C. | a(a2-a)=a2 | D. | $\root{3}{8}=2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批圆珠笔的寿命 | |
| B. | 了解全国九年级学生身高的现状 | |
| C. | 考察人们保护海洋的意识 | |
| D. | 检查一枚用于发射卫星的运载火箭的各零部件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com