
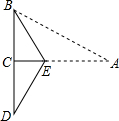
 如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )| A. | 8 | B. | 4 | C. | $\frac{8}{3}$$\sqrt{3}$ | D. | $\frac{4}{3}$$\sqrt{3}$ |
分析 根据勾股定理求出AC的长,根据翻折变换的性质求出CE的长,根据勾股定理求出DE的长.
解答 解:∵∠BCA=90°,BC=4,AB=8,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4$\sqrt{3}$,
由题意得,∠CBE=∠ABE,
∴$\frac{CE}{AE}$=$\frac{BC}{AB}$=$\frac{1}{2}$,
∴CE=$\frac{4}{3}$$\sqrt{3}$,
在Rt△DCE中,DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\frac{8}{3}$$\sqrt{3}$,
故选:C.
点评 本题考查的是翻折变换的性质、勾股定理的应用,找出对应线段和对应角是解题的关键,注意勾股定理在解题中的作用.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
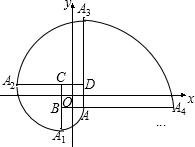 如图,在直角坐标系中,四边形ABCD是正方形,A(1,-1),B(-1,-1),C(-1,1),D(1,1).曲线AA1A2A3…叫做“正方形的渐开线”,其中弧AA1、弧A1A2、弧A2A3、弧A3A4…所在圆的圆心依次是点B、C、D、A循环,则点A2015坐标是(1,4031).
如图,在直角坐标系中,四边形ABCD是正方形,A(1,-1),B(-1,-1),C(-1,1),D(1,1).曲线AA1A2A3…叫做“正方形的渐开线”,其中弧AA1、弧A1A2、弧A2A3、弧A3A4…所在圆的圆心依次是点B、C、D、A循环,则点A2015坐标是(1,4031).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3,y+4) | B. | (x+3,y-4) | C. | (x-4,y+3) | D. | (x+4,y-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛掷一枚硬币,四次中有两次正面朝上 | |
| B. | 打开电视正在播放NBA球赛 | |
| C. | 在标准大气压下,温度低于0℃时冰融化 | |
| D. | 367人中有两人生日相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票张数 | 1~50张 | 51~100张 | 100张以上 |
| 每张票的价格 | 13元 | 11元 | 9元 |
| x=46 | 40<x≤50 | 50<x<54 | |
| 九年级一班购票费/元 | 13×46 | 13x | 11x |
| 九年级二班购票费/元 | 11×(104-46) | 11(104-x) | 11(104-x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com