
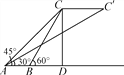
【题目】如图,两个观察者从A,B两地观测空中C处一个气球,分别测得仰角为45°和60°.已知A,B两地相距100 m.当气球沿与AB平行的路线飘移20 s后到达点C′,在A处测得气球的仰角为30°.求:
(1)气球飘移的平均速度(精确到0.1 m/s);
(2)在B处观测点C′的仰角(精确到度).
【答案】(1)气球飘移的平均速度为8.7 m/s;(2)在B处观测点C′的仰角为37°.
【解析】试题首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形,应利用其公共边构造等量关系,进而可求出答案.
试题解析:解:(1)作CD⊥AB,C1E⊥AB,垂足分别为D、E.在Rt△ACD中,AD=CD÷tan∠CAD=CD÷tan45°=CD;在Rt△BCD中,BD=CD÷tan∠CBD=CD÷tan60°=![]() ;
;
又因为AB=AD﹣BD=200,所以CD﹣![]() =200,解得:CD=100(3
=200,解得:CD=100(3![]() ),又CD⊥AB,C1E⊥AB,CC1∥AB,所以C1E=CD,DE=CC1.在Rt△AEC1中,AE=C1E÷tan∠C1AE=100(3+
),又CD⊥AB,C1E⊥AB,CC1∥AB,所以C1E=CD,DE=CC1.在Rt△AEC1中,AE=C1E÷tan∠C1AE=100(3+![]() )÷tan30°=300(
)÷tan30°=300(![]() ),所以CC1=DE=AE﹣AD=300(
),所以CC1=DE=AE﹣AD=300(![]() )﹣100(3+
)﹣100(3+![]() ),即CC1=200
),即CC1=200![]() ,速度为200
,速度为200![]() ÷40≈8.66m/s;
÷40≈8.66m/s;
(2)由(1)知BD=![]() =100(1
=100(1![]() ),所以tan∠C1BE=
),所以tan∠C1BE=![]() =
=![]() ≈0.7637,所以∠C1BE=37°,即仰角为37°.
≈0.7637,所以∠C1BE=37°,即仰角为37°.



科目:初中数学 来源: 题型:
【题目】如图,已知平形四边形ABCD中,对角线AC,BD交点O,E是BD延长线上的点,且△ACE是等边三角形.
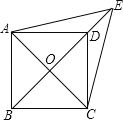
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,AB=2![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
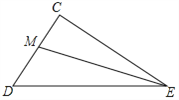
【题目】如图, ![]() ,EM平分
,EM平分![]() ,并与CD边交于点M.DN平分
,并与CD边交于点M.DN平分![]() ,
,
并与EM交于点N.
(1)依题意补全图形,并猜想![]() 的度数等于 ;
的度数等于 ;
(2)证明以上结论.
证明:∵ DN平分![]() ,EM平分
,EM平分![]() ,
,
∴![]() ,
,
![]() = .
= .
(理由: )
∵![]() ,
,
∴![]() = ×(∠ +∠ )= ×90°= °.
= ×(∠ +∠ )= ×90°= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
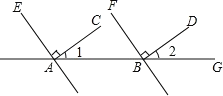
【题目】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以___∥___( ).
又因为AC⊥AE(已知),所以∠EAC=90°( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=__ °.
所以∠EAB=∠FBG( ).
所以___∥___(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提倡节约用水,我县自来水公司每月只给某单位计划内用水200吨,计划内用水每吨收费2.4元,超计划部分每吨按3.6元收费.
⑴用代数式表示下列问题(最后结果需化简 ):设用水量为![]() 吨,当用水量小于等于200吨时,需付款多少元?当用水量大于200吨时,需付款多少元?
吨,当用水量小于等于200吨时,需付款多少元?当用水量大于200吨时,需付款多少元?
⑵若某单位4月份缴纳水费840元,则该单位用水量多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读第①小题的计算方法,再计算第②小题.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com