
【题目】如图,已知平形四边形ABCD中,对角线AC,BD交点O,E是BD延长线上的点,且△ACE是等边三角形.
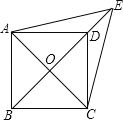
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,AB=2![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
【答案】(1)见解析;(2)四边形ABCD的面积为20.
【解析】
(1)由平行四边形的性质得出AO=OC,由等边三角形三线合一的性质得出EO⊥AC,即BD⊥AC,根据对角线互相垂直的平行四边形是菱形即可得出结论;
(2)由题意易得∠DAO=∠EAO-∠EAD=45°,进而证得菱形是正方形,即可得出结果.
(1)证明:∵四边形ABCD是平行四边形,
∴AO=OC,
∵△ACE是等边三角形,
∴EO⊥AC,
即 BD⊥AC,
∴四边形ABCD是菱形;
(2)解:∵△ACE是等边三角形,
∴∠EAC=60°,
由(1)知,EO⊥AC,AO=OC,
∴∠AEO=∠CEO=30°,△AOE是直角三角形,
∴∠EAO=60°,
∵∠AED=2∠EAD,
∴∠EAD=15°,
∴∠DAO=∠EAO﹣∠EAD=45°,
∵ABCD是菱形,
∴∠BAD=2∠DAO=90°,
∴菱形ABCD是正方形,
∴四边形ABCD的面积=AB2=(2![]() )2=20.
)2=20.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】南开两江中学校初一年级在3月18日听了一堂“树的畅想”的景观设计课,随后在本年级学生中进行了活动收获度调查,采取随机抽样的调查方式进行网络问卷调查,问卷调查的结果分为“非常有收获”“比较有收获”“收获一般”“没有太大的收获”四个等级,分别记作A、B、C、D并根据调查结果绘制两幅不完整统计图:
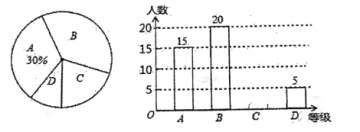
(1)这次一共调查了_______名学生,并将条形统计图补充完整
(2)请在参与调查的这些学生中,随机抽取一名学生,求抽取到的学生对这次“树的畅想”的景观设计课活动收获度是“收获一般”或者“没有太大的收获”的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量![]() (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求![]() 关于
关于![]() 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上有A 、B、C三个点,点A表示的数是-4,点B表示的数是-2,点C表示的数是2.
(1)在数轴上把A 、B、C三点表示出来,并比较各数的大小(用“<”连接);
(2)如何移动点B,使它到点A和点C的距离相等 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背最资料)
低碳生活的理念已逐步被人们所接受,据有关资料统计,一个人平均一年节约的用电相当于减排二氧化碳约18kg;一个人平均一年少买的衣服,相当于减排二氧化碳6kg.
(问题解决)
甲校对本校师生提出“节约用电”的倡议,乙校对本校师生提出“少买衣服”的倡议,2017年两校响应本校倡议的共有1000人,因此而减排二氧化碳总量约13200kg.问:2017年甲、乙两校响应倡议的人数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一直重型运输卡车P沿道路ON方向行驶的速度为18千米/时.

(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
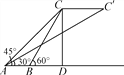
【题目】如图,两个观察者从A,B两地观测空中C处一个气球,分别测得仰角为45°和60°.已知A,B两地相距100 m.当气球沿与AB平行的路线飘移20 s后到达点C′,在A处测得气球的仰角为30°.求:
(1)气球飘移的平均速度(精确到0.1 m/s);
(2)在B处观测点C′的仰角(精确到度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com