
【题目】如图,已知在△ABC中,AB=AC,AD⊥BC于D,且AD=BC=4,若将三角形沿AD剪开成为两个三角形,在平面上把这两个三角形拼成一个四边形,你能拼出所有的不同形状的四边形吗?画出所拼四边形的示意图(标出图中的直角),并分别写出所拼四边形的对角线的长.(只需写出结果即可)
科目:初中数学 来源: 题型:
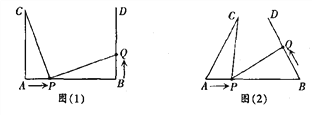
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
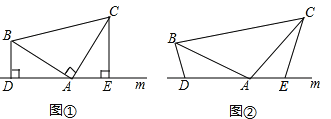
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物线y=x2+bx+c经过A、C两点.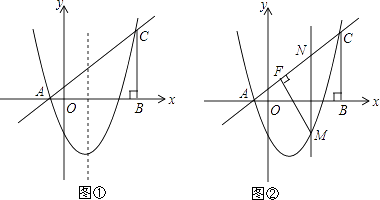
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P,Q分别向x轴作垂线,垂足为点D,E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=x+1与x、y 轴分别交于点A、B,在直线 AB上截取BB1=AB,过点B1分别作x、y 轴的垂线,垂足分别为点A1、C1,得到矩形OA1B1C1;在直线 AB上截取B1B2= BB1,过点B2分别作x、y 轴的垂线,垂足分别为点A2 、C2,得到矩形OA2B2C2;在直线AB上截取B2B3= B1B2,过点B3分别作x、y 轴的垂线,垂足分别为点A3、C3,得到矩形OA3B3C3;……;
则点B1的坐标是 ;第3个矩形OA3B3C3的面积是 ;
第n个矩形OAnBnCn的面积是 (用含n的式子表示,n是正整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D. 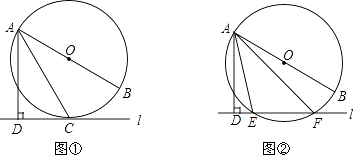
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB;
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
⑴试说明:BE=CF;
⑵若AF=3,BC=4,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次军事演习中,蓝方在﹣条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截.红方行驶2000米到达C后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同距离,刚好在D处成功拦截蓝方.
(1)求点C到公路的距离;
(2)求红蓝双方最初的距离.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com