
【题目】(1)问题发现:如图1,在等边![]() 中,点
中,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .则
.则![]() 与
与![]() 的数量关系是_____,
的数量关系是_____,![]() 的度数为______.
的度数为______.
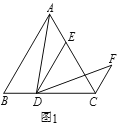
(2)拓展探究:如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,当∠ADF=∠ACF=90°时,求
,当∠ADF=∠ACF=90°时,求![]() 的值.
的值.
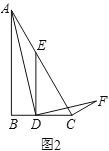
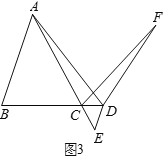
(3)解决问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,直接写出当
,直接写出当![]() 时
时![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意可证△DEC是等边三角形,∠AED=120°,可得DE=DC,由旋转性质可得∠ADF=60°=∠EDC,AD=DF,由“SAS”可证△ADE≌△FDC,可得AE=CF,∠AED=∠DCF=120°,可得∠ACF=60°;
(2)通过证明△DAE∽△DFC,可得![]() ,通过证明△EDC∽△ABC,可得
,通过证明△EDC∽△ABC,可得![]() ,即可求
,即可求![]() 的值;
的值;
(3)通过证明△DAE∽△DFC,可得![]() ,通过证明△EDC∽△ABC,可得
,通过证明△EDC∽△ABC,可得![]() ,即可求的值
,即可求的值![]() ;
;
解:(1)∵DE∥AB
∴∠ABC=∠EDC=60°,∠BAC=∠DEC=60°
∴△DEC是等边三角形,∠AED=120°
∴DE=DC,
∵将AD绕点D顺时针旋转60°得到DF,
∴∠ADF=60°=∠EDC,AD=DF
∴∠ADE=∠FDC,且CD=DE,AD=DF
∴△ADE≌△FDC(SAS)
∴AE=CF,∠AED=∠DCF=120°
∴∠ACF=60°,
故答案为AE=CF,60°
(2)∵∠ABC=90°,∠ACB=60°,
∴∠BAC=30°
∴tan∠BAC= ![]()
∵DE∥AB
∴∠EDC=∠ABC=90°
∵∠ADF=90°,
∴∠ADE=∠FDC
∵∠ACF=90°,∠AED=∠EDC+∠ACB,∠FCD=∠ACF+∠ACB
∴∠AED=∠FCD,且∠ADE=∠FDC
∴△DAE∽△DFC
![]()
∵DE∥AB
∴△EDC∽△ABC
![]()
![]()
(3)∵AB∥DE
∴∠ABC=∠BDE=∠ADF,∠BAC=∠E
∴∠BDE+∠ADB=∠ADF+∠ADB
∴∠ADE=∠CDF,
∵∠ACD=∠ABC+∠BAC=∠ACF+∠DCF,且∠ACF=∠ABC
∴∠BAC=∠DCF=∠E,且∠ADE=∠CDF
∴△ADE∽△FDC
![]()
∵DE∥AB
∴△EDC∽△ABC
![]()
∵![]()
![]()


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】若用“*”表示一种运算规则,我们规定:a*b=ab﹣a+b,如:3*2=3×2﹣3+2=5.以下说法中错误的是( )
A. 不等式(﹣2)*(3﹣x)<2的解集是x<3
B. 函数y=(x+2)*x的图象与x轴有两个交点
C. 在实数范围内,无论a取何值,代数式a*(a+1)的值总为正数
D. 方程(x﹣2)*3=5的解是x=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为∠α=48°和∠β=65°,矩形建筑物宽度AD=20m,高度CD=30m,则信号发射塔顶端到地面的高度FG为__米(结果精确到1m).
参考数据:sin48°=0.7,cos48°=0.7,tan48°=1.1,cos65°=0.4,tan65°=2.1
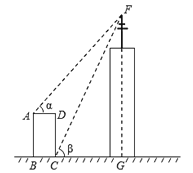
查看答案和解析>>
科目:初中数学 来源: 题型:
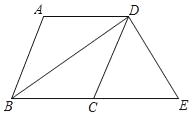
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
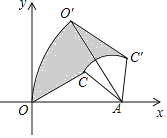
【题目】如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1,![]() ),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
类别 | 成绩 | 频数 |
甲 | 60≤m<70 | 5 |
乙 | 70≤m<80 | a |
丙 | 80≤m<90 | 10 |
丁 | 90≤m≤100 | 5 |

根据图表信息,回答下列问题:
(1)该班共有学生________人;表中a=________;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
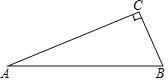
【题目】如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() ,
,![]() 分别是正方形
分别是正方形![]() 的边
的边![]() ,
,![]() 上的点,且
上的点,且![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)若![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 为
为![]() 的中点;
的中点;
(3)连接![]() ,设
,设![]() ,
,![]() ,
,![]() ,在(2)的条件下,判断
,在(2)的条件下,判断![]() 是否成立?并说明理由.
是否成立?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com