
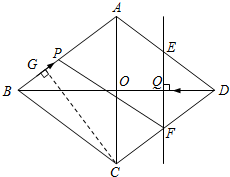
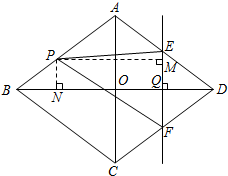
 ��ͼ��������ABCD�У�AC��BD���ڵ�O��AC=12cm��BD=16cm������P���߶�AB�ϣ���B��A�˶����ٶ�Ϊ1cm/s������Q���߶�OD�ϣ���D��O�˶����ٶ�Ϊ1cm/s������Q��ֱ��EF��BD��AD��E����CD��F������PF�����˶�ʱ��Ϊt��0��t��8�����ʣ�
��ͼ��������ABCD�У�AC��BD���ڵ�O��AC=12cm��BD=16cm������P���߶�AB�ϣ���B��A�˶����ٶ�Ϊ1cm/s������Q���߶�OD�ϣ���D��O�˶����ٶ�Ϊ1cm/s������Q��ֱ��EF��BD��AD��E����CD��F������PF�����˶�ʱ��Ϊt��0��t��8�����ʣ�| 1 |
| 2 |
| 1 |
| 2 |
| DF |
| DC |
| QD |
| OD |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 62+82 |
| DF |
| DC |
| QD |
| OD |
| DF |
| 10 |
| t |
| 8 |
| 5 |
| 4 |
| 5 |
| 4 |
| 40 |
| 9 |
| 40 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| 48 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 48 |
| 5 |
| 6 |
| 5 |
| QD |
| OD |
| QF |
| OC |
| t |
| 8 |
| QF |
| 6 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 6 |
| 5 |
| 3 |
| 4 |
| 3 |
| 4 |
| 6 |
| 5 |
| 3 |
| 4 |
| 6 |
| 5 |
| 17 |
| 40 |
| 12 |
| 5 |
| PN |
| AO |
| PB |
| AB |
| BN |
| BO |
| PN |
| 6 |
| 4 |
| 10 |
| BN |
| 8 |
| 12 |
| 5 |
| 16 |
| 5 |
| 12 |
| 5 |
| 3 |
| 5 |
| 16 |
| 5 |
| 44 |
| 5 |
| PM2+EN2 |
| ||
| 5 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| 5 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
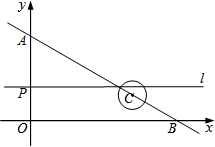 ��ͼ��ƽ��ֱ������ϵ�ij��ȵ�λ�����ף�ֱ��l�ֱ���x�ᡢy���ཻ��B��A���㣬��OA=6����ABO=30�㣬��C������BA����3����/����ٶ��˶�����C��ΪԲ�����뾶Ϊ1���ġ�C����P��2����/����ٶ����߶�OA�������˶�������P��ֱ��l��x�ᣮ����C���Pͬʱ�ӵ�B����O��ʼ�˶������˶�ʱ��Ϊt�룬���������˶�������ֱ��l���C����ʱt��ֵΪ
��ͼ��ƽ��ֱ������ϵ�ij��ȵ�λ�����ף�ֱ��l�ֱ���x�ᡢy���ཻ��B��A���㣬��OA=6����ABO=30�㣬��C������BA����3����/����ٶ��˶�����C��ΪԲ�����뾶Ϊ1���ġ�C����P��2����/����ٶ����߶�OA�������˶�������P��ֱ��l��x�ᣮ����C���Pͬʱ�ӵ�B����O��ʼ�˶������˶�ʱ��Ϊt�룬���������˶�������ֱ��l���C����ʱt��ֵΪ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com