
����Ŀ��ijУΪ���˽�ѧ���İ�ȫ��ʶ����ȫУ��Χ�������ȡ����ѧ�������ʾ����飮���ݵ���������ѧ���İ�ȫ��ʶ�ֳɡ�����������һ�㡱������ǿ��������ǿ���ĸ���Σ����������������в�������ͳ��ͼ��
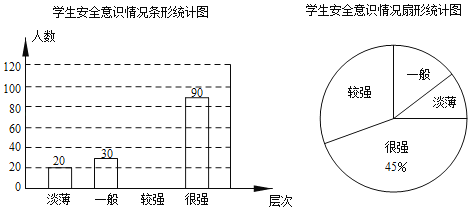
����������Ϣ������������⣺
��1����ε���һ����ȡ���� ����ѧ����������ͳ��ͼ����������
��2������ͳ��ͼ�У�����ǿ�������ռԲ�ĽǵĴ�СΪ�� ���㣻
��3������У��1900��ѧ������Ҫ��ȫ��ʶΪ������������һ�㡱��ѧ��ǿ����ȫ���������ݵ��������������ȫУ��Ҫǿ����ȫ������ѧ��������
���𰸡���1��200����ͼ����������2��108����3��ȫУ��Ҫǿ����ȫ������ѧ����475�ˣ�
��������
��1���ɰ�ȫ��ʶΪ����ǿ����ѧ��������ռ�İٷֱȵõ���ȡѧ�������������������ֱ��ȥ��ȫ��ʶ������������һ�㡱������ǿ�����������ó���ȫ��ʶΪ����ǿ����ѧ��������ȫ����ͳ��ͼ���ɣ�
��2����360������ȫ��ʶΪ����ǿ����ѧ��ռ�İٷֱȼ��ɣ�
��3���ɰ�ȫ��ʶΪ������������һ�㡱��ѧ��ռ�İٷֱȵĺͣ�����1900���ɵõ������
��1����ε����ˣ�90��45%��200��������
���С���ǿ����ʶ��ѧ���У�200��20��30��90��60���ˣ���
�ʴ�Ϊ��200��
��ȫ������ͳ��ͼ��ͼ��ʾ��
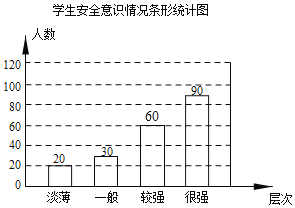 ��
��
��2������ͳ��ͼ�У�����ǿ�������ռԲ�ĽǵĴ�СΪ360���![]() ��108�㣬
��108�㣬
�ʴ�Ϊ��108��
��3��1900��![]() ��475���ˣ�
��475���ˣ�
��ȫУ��Ҫǿ����ȫ������ѧ����475�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() Ϊ�Ż�
Ϊ�Ż�![]() �ϵĶ��㣨�����
�ϵĶ��㣨�����![]() ��
��![]() �غϣ����ڵ�
�غϣ����ڵ�![]() �˶��Ĺ����У����½�����ȷ���ǣ� ��
�˶��Ĺ����У����½�����ȷ���ǣ� ��

A.![]() �Ĵ�С�ı�B.��
�Ĵ�С�ı�B.��![]() ����
����![]() ����ֱ�ߵľ���������ֵ
����ֱ�ߵľ���������ֵ
C.�߶�![]() ��
��![]() �ij���֮�Ͳ���D.ͼ����Ӱ���ֵ��������
�ij���֮�Ͳ���D.ͼ����Ӱ���ֵ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ�Ľ�����еΪ���Ż���ʹ�÷���Ϊ�����������Ȳ���ǰ������˫����ֱ֮��Ȼ�����������գ�ͼ2Ϊʾ��ͼ����֪![]() �ڳ�ʼλ�ã�
�ڳ�ʼλ�ã�![]() , ��
, ��![]() ��ͬһֱ���ϣ�
��ͬһֱ���ϣ�![]() ��
��

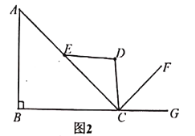
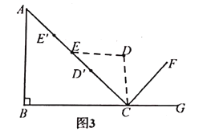
��1����![]() �ڳ�ʼλ��ʱ�����
�ڳ�ʼλ��ʱ�����![]() ��
��![]() �ľ��룻
�ľ��룻
��2����˫����ֱ����ͼ3����![]() �ֱ�ӳ�ʼλ���˶�����
�ֱ�ӳ�ʼλ���˶�����![]() �� ����
�� ����![]() ���㹲�ߣ����ʱ��
���㹲�ߣ����ʱ��![]() ��������ֱ�߶ȣ� ( �����ȷ����λ) (�ο�����:
��������ֱ�߶ȣ� ( �����ȷ����λ) (�ο�����:![]()
![]()
![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������β���ͬһԲ���幤���ĺ����ֱ������λ��![]() ������õ����ݷֱ����1����2��
������õ����ݷֱ����1����2��
��1���IJ�������
�������� | 9.8 | 9.9 | 10 | 10.1 | 10.3 |
Ƶ�� | 1 | 3 | 3 | 2 | 1 |
��2���ҵIJ�������
�������� | 9.7 | 9.8 | 10 | 10.1 | 10.3 |
Ƶ�� | 1 | 2 | 3 | 2 | 2 |
��1���������Щ����������ѡ��һ��������Ϊ����ֱ���Ĺ���ֵ��Ӧ�����Ǹ����ݣ���˵������.
��2��������ٲ���һ�Σ�����������������ǡ���ǹ���ֵ�ĸ��ʣ�
��3����ֱ���жϼ�������˭�IJ�����������______������ң�����ѡ���ͳ������_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
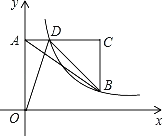
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��y���������ϣ�AC��x�ᣬ��B��C�ĺ����궼��3����BC��2����D��AC�ϣ�������������y��![]() ��x��0����ͼ����B��D����AO��BC��3��2��
��x��0����ͼ����B��D����AO��BC��3��2��
��1�����D���ꣻ
��2������AOD����OD�۵����趥��A�ĶԳƵ�ΪA�䣬���жϵ�A���Ƿ�ǡ������ֱ��BD�ϣ�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������
������ⳣ����Ҫ�������ߣ�����ƽ��ͼ������Ҫ���������߲��ԣ�
�������龳��
��ͼ1����������ABCD�У�E��F��G�ֱ���BC��AB��CD�ϵĵ㣬FG��AE�ڵ�Q����֤��AE��FG��
С���ڷ�������˼·ʱ�뵽������ƽ�Ʒ���
����1��ƽ���߶�FGʹ��F���B�غϣ�����ȫ�������Σ�
����2��ƽ���߶�BCʹ��B���F�غϣ�����ȫ�������Σ�
������Ӧ�ã�
��1���밴��С����˼·��ѡ������һ�ַ�������֤����
��2����ͼ2�������������У���A��B��C��DΪ��㣬AB��CD�ڵ�O����tan��AOC��ֵ��
��3����ͼ3����P���߶�AB�ϵĶ��㣬�ֱ���AP��BPΪ����AB��ͬ����������APCD��������PBEF������DE�ֱ��߶�BC��PC�ڵ�M��N��
������DMC�Ķ�����
������AC��DE�ڵ�H����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
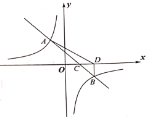
����Ŀ��һ�κ���![]() ��ͼ����˫����
��ͼ����˫����![]()
![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬��
���㣬��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ������
������![]() ��
��![]() �ᣬ����Ϊ��
�ᣬ����Ϊ��![]() ��
��
��1����һ�κ����Ľ���ʽ��
��2������ͼ��ֱ��д������ʽ![]() �Ľ⼯��
�Ľ⼯��
��3��![]() �����Ϊ
�����Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯ѧ���μӹ��������ݸ�У���꼶�������ͬѧij���ڲμӹ������˴��������˵�����ͳ��ͼ(��ͼ��ʾ),������˵����ȷ����( )
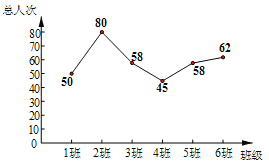
A.������40B.ƽ������60C.������58D.��λ����51.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڼ�ijУѧ�������ۿ�����ֱ���γ̣�Ϊ���˽�ȫУ500��ѧ���ۿ�����ֱ���γ̵�����������ȡ50��ѧ���������ǹۿ�����ֱ���γ̵Ľ��������ռ����������ݽ����������������ͷ�������������˲�����Ϣ��
�ۿ�ֱ���ν�����Ƶ���ֲ���
����x | Ƶ�� | Ƶ�� |
| 8 | 0.16 |
| 10 | 0.20 |
| 16 |
|
|
| 0.24 |
| 4 | 0.08 |
���� | 50 | 1 |

���У�������![]() ��һ��������ǣ�
��һ��������ǣ�
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
�����������Ϣ������������⣺
��1��![]() __________��
__________��![]() __________
__________
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�������ȡ��50��ѧ���ۿ�ֱ���ν�������λ����___________��
��4������Ƹ�Уѧ���йۿ�����ֱ���ν���������30�ε�Լ��__________�ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com