
【题目】在平面直角坐标系中,二次函数y=-x2-bx+c的图象经过点A,点B(1,0)和点C(0,3).点D是抛物线的顶点.
(1)求二次函数的解析式和点D的坐标
(2)直线y=kx+n(k≠0)与抛物线交于点M,N,当△CMN的面积被y轴平分时,求k和n应满足的条件
(3)抛物线的对称轴与x轴交于点E,将抛物线向下平移m(m>0)个单位,平移后抛物线与y轴交于点C′,连接DC′,OD,是否存在OD平分∠C′DE的情况?若存在,求出m的值;若不荐在,请说明理由.
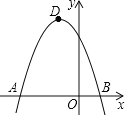
【答案】(1)y=-x2-2x+3,点D(-1,4);(2)k=-2,n<3;(3)存在,m=![]() .
.
【解析】
(1)利用待定系数法求得解析式,利用二次函数的顶点坐标公式即可求得点D的坐标;
(2)联立直线与抛物线的解析式得出关于x的一元二次方程,根据要使y轴平分△CMN的面积,则M、N两点的横坐标互为相反数,根据根与系数的关系即可得出k值;再根据而点H在点C之下这一条件,可得出n的取值范围;
(3)解答本类题目的总体思路在于先假设存在,若能求出m的值则假设成立,否则不成立;若存在,首先根据角平分线的性质,得出OH= 1,DH= 4;进而设HG=a,由△DOG的面积建立关于a的方程组,解之可得点G的坐标,进而求出直线DG的表达式和OC′,与OC作差,即可求出m的值,说明存在OD平分∠C′DE的情况.
(1)y=-x2-bx+c=-x2-bx+3,将点B坐标代入上式得:0=-1-b+3,
解得:b=2,
故抛物线的表达式为:y=-x2-2x+3,
则点A(-3,0)、点D(-1,4);
(2)设点M、N的横坐标为x1、x2,
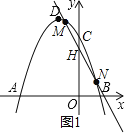
当△CMN的面积被y轴平分时,则x1+x2=0,
将二次函数表达式与直线表达式联立并整理得:
x2+(2+k)x+(n-3)=0,
x1+x2=-(2+k)=0,即k=-2,
而点H在点C之下,故n<3,
故:k=-2,n<3;
(3)存在,理由:
OD平分∠C′DE,即:∠EDO=∠ODC′,
延长DC′交x轴于点G,过点O作OH⊥DG交于H,
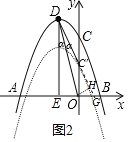
∵∠EDO=∠ODC′,
∴OH=OE=1,DH=DE=4,
设HG=a,则OG=![]() ,
,
S△DOG=![]() OG×DE=
OG×DE=![]() OH×GD,
OH×GD,
即:4![]() =1×(4+a),
=1×(4+a),
解得:a=![]() ,即点G(
,即点G(![]() ,0),
,0),
∴直线DG的表达式为:y=-![]() x+
x+![]() ,
,
即OC′=![]() ,
,
m=3-![]() =
=![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在圆O中,弦AB与CD相交于点E,且弧AC与弧BD相等.点D在劣弧AB上,联结CO并延长交线段AB于点F,联结OA、OB.当OA=![]() ,且tan∠OAB=
,且tan∠OAB=![]() .
.
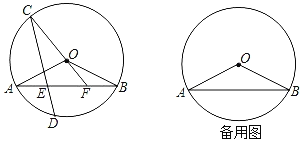
(1)求弦CD的长;
(2)如果△AOF是直角三角形,求线段EF的长;
(3)如果S△CEF=4S△BOF,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:把一次函数y=kx+b的一次项系数和常数项互换得y=bx+k,我们称y=kx+b和y=bx+k(其中k·b≠0,且|k|≠|b|))为互助一次函数,例如:y=-2x+3和y=3x-2就是互助一次函数.如图1所示,一次函数y=kx+b和它的互助一次函数的图象![]() 1,
1,![]() 2交于点P,
2交于点P,![]() 1,
1,![]() 2与x轴、y轴分别交于点A,B和点C,D.
2与x轴、y轴分别交于点A,B和点C,D.
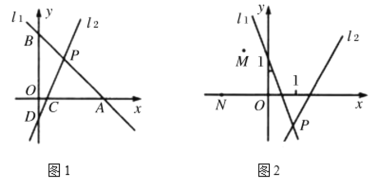
(1)如图1所示,当k=-1,b=5时,直接写出点P的坐标是_________.
(2)如图2所示,已知点M(-1,1.5),N(-2,0).试探究随着k,b值的变化,MP+NP的值是否发生变化,若不变,求出MP+NP的值;若变化,求出使MP+NP取最小值时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(-2,m)绕坐标原点O顺时针旋转90°后,恰好落在图中⊙P中的阴影区域(包括边界)内,⊙P的半径为1,点P的坐标为(3,2),则m的取值范围是______.
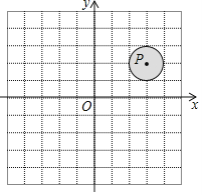
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店以每件50元的价格购进![]() 两种服装,已知销售30件
两种服装,已知销售30件![]() 种服装和40件
种服装和40件![]() 种服装共获利润1000元,销售40件
种服装共获利润1000元,销售40件![]() 种服装和50件
种服装和50件![]() 种服装共获利润1300元.
种服装共获利润1300元.
(1)求两种服装每件的售价;
(2)若该服装店准备购进![]() 两种服装共80件,并规定
两种服装共80件,并规定![]() 种服装不少于
种服装不少于![]() 种服装的
种服装的![]() ,设购进
,设购进![]() 种服装
种服装![]() 件,求利润
件,求利润![]() (元)与
(元)与![]() (件)之间的函数解析式,并求出当
(件)之间的函数解析式,并求出当![]() 取何值时,利润最大,最大利润为多少?
取何值时,利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P,已知BC=6,AH=4.当矩形DEFG面积最大时,HP的长是( )
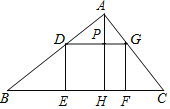
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校数学课外实践小组对这些交通法规的了解情况在全校随机调查了部分学生,调查结果分为四种:A.非常了解,B.比较了解,C.基本了解,D.不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
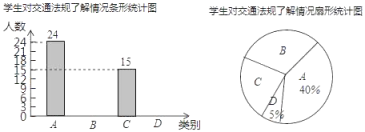
请结合图中所给信息解答下列问题:
(1)本次共调查 名学生;扇形统计图中C所对应扇形的圆心角度数是 ;
(2)补全条形统计图;
(3)学校准备从组内的甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛,请用列表或画树状图的方法求丙和丁两名学生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,
,
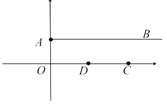
(1)若![]() ,点
,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上,当
上,当![]() 是边长为5的等腰三角形,共有几个这样的点
是边长为5的等腰三角形,共有几个这样的点![]() ,并尝试求出点
,并尝试求出点![]() 的坐标;
的坐标;
(2)若直线![]() 与
与![]() 不平行,
不平行,![]() 在直线
在直线![]() 上,是否存在点
上,是否存在点![]() ,使得
,使得![]() 是直角三角形,且
是直角三角形,且![]() ,若存在,求出这样的点
,若存在,求出这样的点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com