
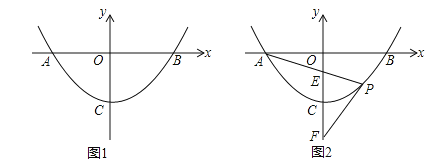
【题目】抛物线![]() 与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
【答案】(1)①![]() ;②D(﹣1,﹣3)或(
;②D(﹣1,﹣3)或(![]() ,
,![]() );(2)定值为2.
);(2)定值为2.
【解析】
试题分析:(1)①根据待定系数法求函数解析式,可得答案;②根据平行线的判定,可得PD∥OB,根据函数值相等两点关于对称轴对称,可得D点坐标;
(2)根据待定系数法,可得E、F点的坐标,根据分式的性质,可得答案.
试题解析:(1)①将P(1,﹣3),B(4,0)代入![]() ,得:
,得:![]() ,解得:
,解得: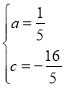 ,抛物线的解析式为
,抛物线的解析式为![]() ;
;
②如图1,由∠DPO=∠POB,得:DP∥OB,D与P关于y轴对称,P(1,﹣3),得D(﹣1,﹣3);
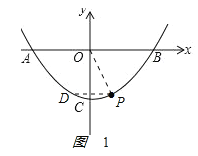
如图,D在P右侧,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,设Q(q,0),则![]() ,解得:q=5,∴Q(5,0),则直线PD2为
,解得:q=5,∴Q(5,0),则直线PD2为![]() ,再联立
,再联立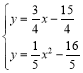 ,解得:x=1或
,解得:x=1或![]() ,∴ D2(
,∴ D2(![]() ,
,![]() ).
).
综上所述,点D的坐标为(-1,-3)或(![]() ,
,![]() ).
).

(2)点P运动时,![]() 是定值,设P点坐标为(m,
是定值,设P点坐标为(m,![]() ),A(﹣4,0),B(4,0),设AP的解析式为y=kx+b,将A、P点坐标代入,得:
),A(﹣4,0),B(4,0),设AP的解析式为y=kx+b,将A、P点坐标代入,得: ,解得b=
,解得b=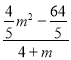 =
=![]() ,即E(0,
,即E(0,![]() ),设BP的解析式为y=k1x+b1,将B、P点坐标代入,得:
),设BP的解析式为y=k1x+b1,将B、P点坐标代入,得:
,解得b2= =
=![]() ,即F(0,
,即F(0,![]() ),OF+OE=
),OF+OE=![]() =
=![]() ,
,![]() =
=![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】如图①,直线![]() 交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
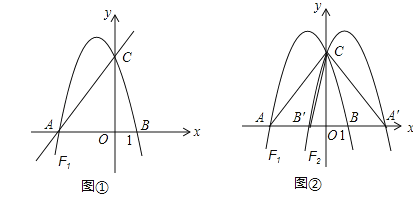
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m为常数,﹣1≤m≤4).A(﹣m﹣1,
(m为常数,﹣1≤m≤4).A(﹣m﹣1,![]() ),B(
),B(![]() ,
,![]() ),C(﹣m,
),C(﹣m,![]() )是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
(1)用含m的代数式表示抛物线的顶点坐标;
(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;
(3)当1<PH≤6时,试比较![]() ,
,![]() ,
,![]() 之间的大小.
之间的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为假命题的是( )
A. 三角形三个内角的和等于180° B. 三角形两边之和大于第三边
C. 三角形的外角大于任何一个和它不相邻的内角 D. 若a>0,b<0,则a+b>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com