
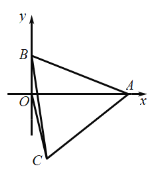
【题目】如图,在直角坐标系中,已知点A(6,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下作等边△ABC,连接OC,则OC的最小值( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
以OA为对称轴作等边△AMN,由“SAS”可证△ANC≌△AMB,可得∠AMB=∠ANC=60°,由直角三角形的性质可求∠AEN=30°,EO= ![]() ON=6,则点C在EN上移动,当OC'⊥EN时,OC'有最小值,即可求解.
ON=6,则点C在EN上移动,当OC'⊥EN时,OC'有最小值,即可求解.
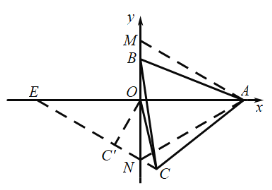
解:如图,以OA为对称轴作等边△AMN,延长CN交x轴于E,
∵△ABC是等边三角形,△AMN是等边三角形,
∴AM=AN,AB=AC,∠MAN=∠BAC,∠AMN=60°=∠ANM, ∴∠BAM=∠CAN,
∴△ANC≌△AMB(SAS),
∴∠AMB=∠ANC=60°,
∴∠ENO=60°,
∵AO=6,∠AMB=60°,AO⊥BO,
∴MO=NO=![]()
∵∠ENO=60°,∠EON=90°,
∴∠AEN=30°,EO=![]() ON=6,
ON=6,
∴点C在EN上移动,
∴当OC'⊥EN时,OC'有最小值,
此时,O'C=![]() EO=3,
EO=3,
故选:B.


科目:初中数学 来源: 题型:
【题目】某学校为了解九年级的600名学生每天的自主学习情况,随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两副不完整的统计图(图1图2),请根据统计图中的信息回答下列问题:
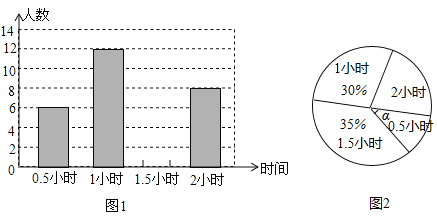
(1)本次调查的学生人数是 人;
(2)图2中角![]() 是 度;
是 度;
(3)将图1条形统计图补充完整;
(4)估算该校九年级学生自主学习不少于1.5小时有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
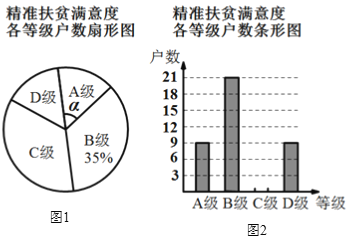
(1)本次抽样调查测试的建档立卡贫困户的总户数______.
(2)图1中,∠α的度数是______,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为![]() )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户
)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校共抽取50名同学参加学校举办的“预防新冠肺炎”知识测验,所得成绩分别记作60分、70分、80分、90分、100分,并将统计结果绘制成不完整的扇形统计图(如图).
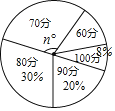
(1)若n=108,则成绩为60分的人数为 ;
(2)若从这50位同学中,随机抽取一人,求抽到同学的分数不低于90分的概率;
(3)若成绩的唯一众数为80分,求这个班平均成绩的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
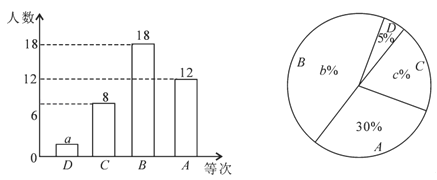
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】崇州(古称蜀州),老子思想创立发扬地,崇州市历史悠久,汉代称蜀川,唐代称蜀州,其建制历史长达4300年,公元316年设立县制,1994年撤县设市.崇州市全市幅员面积1090平方公里,呈“四山一水五分田”格局,是距离成都天府广场最近的郊区区域,是四川省首批命名的历史悠久名城,辖6个街道办事处,9个镇,户籍人口66.48万(其中城镇人口31.6万),常住人口75万,用科学记数法表示75万为( )
A.7.5×104B.75×104C.0.75×106D.7.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
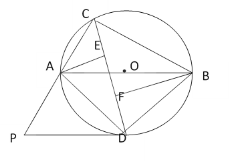
(1)求证:DP∥AB;
(2)试猜想线段AE、EF、BF之间的数量关系,并加以证明;
(3)若AC=6,BC=8,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.
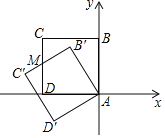
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com