
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
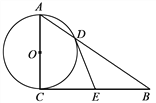
(1)求证:EB=EC;
(2)当△ABC满足什么条件时,四边形ODEC是正方形?证明你的结论.
【答案】详解解析
【解析】试题(1)连接CD,在Rt△ABC中,∠ACB=90°,AC为直径即可判定BC是⊙O的切线,所以∠ADC=90°,根据切线长定理可得DE=CE,根据等腰三角形的性质可得∠DCE=∠CDE,再由∠DCE+∠EBD=∠CDE+∠EDB=90°,即可得∠EBD=∠EDB,所以DE=BE,即可得CE =BE;(2)当△ABC是等腰直角三角形时,四边形ODEC是正方形,先证得四边形ODEC是矩形,再由EC=ED,即可判定四边形ODEC是正方形.
试题解析:
(1)证明:连接CD,
∵AC是直径,∠ACB=90°,
∴BC是⊙O的切线,∠ADC=90°.
∵DE是⊙O的切线,
∴DE=CE(切线长定理).∴∠DCE=∠CDE,
又∵∠DCE+∠EBD=∠CDE+∠EDB=90°,
∴∠EBD=∠EDB.∴DE=BE,
∴CE =BE.
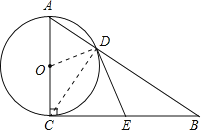
(2)解:当△ABC是等腰直角三角形时,四边形ODEC是正方形. 证明如下:
△ABC是等腰直角三角形.则∠B=45°,
∴∠DCE=∠CDE=45°,则∠DEB=90°,
又∵OC=OD,∠ACB=90°,∴∠OCD=∠ODC=45°,
∴∠ODE=90°,
∴四边形ODEC是矩形,
∵EC=ED,
∴四边形ODEC是正方形.


科目:初中数学 来源: 题型:
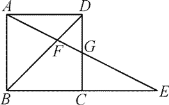
【题目】如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去扬州马可波罗花世界游玩.
![]() 小明和小刚都在本周日上午去游玩的概率为________;
小明和小刚都在本周日上午去游玩的概率为________;
![]() 求他们三人在同一个半天去游玩的概率.
求他们三人在同一个半天去游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点B的坐标为![]() ,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数
,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数![]() 的图象交AB,BC分别于点E,F.
的图象交AB,BC分别于点E,F.
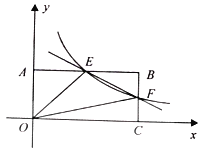
(1)求直线EF的解析式.
(2)求四边形BEOF的面积.
(3)若点P在y轴上,且![]() 是等腰三角形,请直接写出点P的坐标.
是等腰三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=![]() (x>0)和y=
(x>0)和y=![]() (x<0)的图象分别交于点P,Q.
(x<0)的图象分别交于点P,Q.
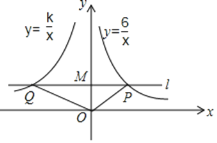
(1)求P点的坐标;
(2)若△POQ的面积为9,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(-4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为( )

A. (0,3)
B. (0,2.5)
C. (0,2)
D. (0,1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
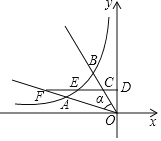
【题目】如图,角α的两边与双曲线y=![]() (k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=
(k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=![]() 、射线OA于点E、F,若OA=2AF,OC=2CB,则
、射线OA于点E、F,若OA=2AF,OC=2CB,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
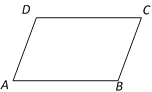
【题目】已知:在平行四边形ABCD中,AB︰BC=3︰2.
(1)根据条件画图:作∠BCD的平分线,交边AB于点E,取线段BE的中点F,连接DF交CE于点G.
(2)设![]() ,那么向量
,那么向量![]() =______.(用向量
=______.(用向量![]() 、
、![]() 表示),并在图中画出向量
表示),并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD 中,对角线AC,BD交于点O,以 AD,OD为邻边作平行四边形ADOE,连接BE.
(1) 求证:四边形AOBE是菱形;
(2) 若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com