
ЁОЬтФПЁПНёФъМйЦкФГаЃЖдВйГЁНјааСЫЮЌаоИФдьЃЌШчЭМЪЧВйГЁЕФвЛНЧ.дкГЄЮЊ![]() УзЃЌПэЮЊ
УзЃЌПэЮЊ![]() УзЕФГЄЗНаЮГЁЕижаМфЃЌВЂХХзХСНИіДѓаЁЯрЭЌЕФРКЧђГЁЃЌетСНИіРКЧђГЁжЎМфвдМАРКЧђГЁгыГЄЗНаЮГЁЕиБпбиЕФОрРыЖМЮЊ
УзЕФГЄЗНаЮГЁЕижаМфЃЌВЂХХзХСНИіДѓаЁЯрЭЌЕФРКЧђГЁЃЌетСНИіРКЧђГЁжЎМфвдМАРКЧђГЁгыГЄЗНаЮГЁЕиБпбиЕФОрРыЖМЮЊ![]() Уз.
Уз.
(1)жБНгаДГівЛИіРКЧђГЁЕФГЄКЭПэЃЛ(гУКЌзжФИ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФДњЪ§ЪНБэЪО)
ЕФДњЪ§ЪНБэЪО)
(2)гУКЌзжФИ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФДњЪ§ЪНБэЪОетСНИіРКЧђГЁеМЕиУцЛ§ЕФКЭЃЌВЂЧѓГіЕБ
ЕФДњЪ§ЪНБэЪОетСНИіРКЧђГЁеМЕиУцЛ§ЕФКЭЃЌВЂЧѓГіЕБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪБЃЌетСНИіРКЧђГЁеМЕиУцЛ§ЕФКЭ.
ЪБЃЌетСНИіРКЧђГЁеМЕиУцЛ§ЕФКЭ.
ЁОД№АИЁП(1)ГЄЃК![]() УзЃЌПэЃК
УзЃЌПэЃК![]() УзЃЛ(2)
УзЃЛ(2)![]() ЃЛ
ЃЛ![]() .
.
ЁОНтЮіЁП
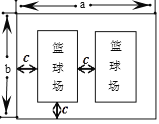
(1) вРОнЬтвтЮФзжУшЪіЃЌПЩвдЭЈЙ§a,b,cСаГіДњЪ§ЪНЗжБ№БэЪОРКЧђГЁЕФГЄКЭПэЃЛ
(2) ИљОнУцЛ§ЙЋЪНСаГіДњЪ§ЪНЛЏМђПЩЕУЃЌДњШыa=42ЃЌ![]() ЃЌ
ЃЌ![]() МДПЩ.
МДПЩ.
НтЃК(1) вРЬтвтПЩЕУЃКГЄЃКЃЈb-2cЃЉУзЃЌ ПэЃК ![]() Уз
Уз
(2) гЩ(1)ЕУЕНЕФГЄКЭПэДњШы S=2ЃЈb-2cЃЉЁС![]() ЃЈa-3cЃЉ=ЃЈb-2cЃЉЃЈa-3cЃЉ=ЃЈab-3bc-2ac+6c2ЃЉm2
ЃЈa-3cЃЉ=ЃЈb-2cЃЉЃЈa-3cЃЉ=ЃЈab-3bc-2ac+6c2ЃЉm2
ДњШыa=42ЃЌ![]() ЃЌ
ЃЌ![]() S=ЃЈ42ЁС36-3ЁС36ЁС4-2ЁС42ЁС4+6ЁС42ЃЉ=1512-432-336+96=840m2
S=ЃЈ42ЁС36-3ЁС36ЁС4-2ЁС42ЁС4+6ЁС42ЃЉ=1512-432-336+96=840m2



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЪ§жсЩЯAЁЂBСНЕуЖдгІЕФЪ§ЗжБ№ЪЧ6ЁЂЉ6ЃЌЁЯDCEЃН90ЁуЃЈCгыOжиКЯЃЌDЕудкЪ§жсЕФе§АыжсЩЯЃЉЃЎ
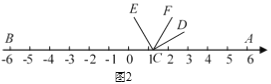
ЃЈ1ЃЉШчЭМ2ЃЌНЋЁЯDCEбиЪ§жсЕФе§АыжсЯђгвЦНвЦtЃЈ0ЃМtЃМ3ЃЉИіЕЅЮЛКѓЃЌдйШЦЕуЖЅЕуCФцЪБеыа§зЊ30tЖШЃЌзїCFЦНЗжЁЯACEЃЌДЫЪБМЧЁЯDCFЃНІСЃЎ
ЂйЕБtЃН1ЪБЃЌЧѓІСЕФЖШЪ§ЃЛ
ЂкВТЯыЁЯBCEКЭІСЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЛ
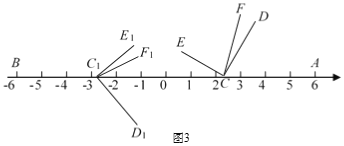
ЃЈ2ЃЉШчЭМ3ЃЌПЊЪМЁЯD1C1E1гыЁЯDCEжиКЯЃЌНЋЁЯDCEбиЪ§жсЕФе§АыжсЯђгвЦНвЦtЃЈ0ЃМtЃМ3ЃЉИіЕЅЮЛЃЌдйШЦЕуЖЅЕуCФцЪБеыа§зЊ30tЖШЃЌзїCFЦНЗжЁЯACEЃЌДЫЪБМЧЁЯDCFЃНІСЃЌгыДЫЭЌЪБЃЌНЋЁЯD1C1E1биЪ§жсЕФИКАыжсЯђзѓЦНвЦtЃЈ0ЃМtЃМ3ЃЉИіЕЅЮЛЃЌдйШЦЕуЖЅЕуC1ЫГЪБеыа§зЊ30tЖШЃЌзїC1F1ЦНЗжЁЯAC1E1ЃЌМЧЁЯD1C1F1ЃНІТЃЌШєІСгыІТТњзу![]() ЃЌЧѓГіДЫЪБtЕФжЕЃЎ
ЃЌЧѓГіДЫЪБtЕФжЕЃЎ
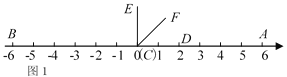
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЬьЃЌФГЭЌбЇдчЩЯ8ЕузјГЕДггрвІЭМЪщЙнГіЗЂШЅФўВЈДѓбЇЃЌЦћГЕРыПЊгрвІЭМЪщЙнЕФОрРы![]() ЃЈЧЇУзЃЉгыЫљгУЪБМф
ЃЈЧЇУзЃЉгыЫљгУЪБМф![]() ЃЈЗжЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪО.вбжЊЦћГЕдкЭОжаЭЃГЕМггЭвЛДЮЃЌдђЯТСаУшЪіВЛе§ШЗЕФЪЧЃЈ ЃЉ
ЃЈЗжЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪО.вбжЊЦћГЕдкЭОжаЭЃГЕМггЭвЛДЮЃЌдђЯТСаУшЪіВЛе§ШЗЕФЪЧЃЈ ЃЉ

A.ЦћГЕдкЭОжаМггЭгУСЫ10Зжжг
B.Шє![]() ЃЌдђМгТњгЭвдКѓЕФЫйЖШЮЊ80ЧЇУз/аЁЪБ
ЃЌдђМгТњгЭвдКѓЕФЫйЖШЮЊ80ЧЇУз/аЁЪБ
C.ШєЦћГЕМггЭКѓЕФЫйЖШЪЧ90ЧЇУз/аЁЪБЃЌдђ![]()
D.ИУЭЌбЇ![]() ЕНДяФўВЈДѓбЇ
ЕНДяФўВЈДѓбЇ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯABDЁЂЁЯACDЕФНЧЦНЗжЯпНЛгкЕуPЃЌШєЁЯA=50ЁуЃЌЁЯD=10ЁуЃЌдђЁЯPЕФЖШЪ§ЮЊЃЈ ЃЉ
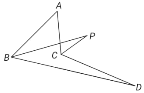
A. 10ЁуB. 15ЁуC. 20ЁуD. 25Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊEЁЂFЗжБ№ЮЊе§ЗНаЮABCDЕФБпABЃЌBCЕФжаЕуЃЌAFгыDEНЛгкЕуMЃЌOЮЊBDЕФжаЕуЃЌдђЯТСаНсТлЃКЂйЁЯAME=90ЁуЃЛЂкЁЯBAF=ЁЯEDBЃЛЂлЁЯBMO=90ЁуЃЛЂмMD=2AM=4EMЃЛЂнAM=![]() MFЃЎЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
MFЃЎЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
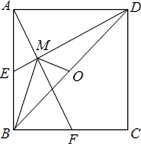
A. 5Иі B. 4Иі C. 3Иі D. 2Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§y=x2+bx+cЃЈbЃЌcЖМЪЧГЃЪ§ЃЉЕФЭМЯѓОЙ§ЕуЃЈ1ЃЌ0ЃЉКЭЃЈ0ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЕБЉ2ЁмxЁм2ЪБЃЌЧѓyЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉвбжЊЕуPЃЈmЃЌnЃЉдкИУКЏЪ§ЕФЭМЯѓЩЯЃЌЧвm+n=1ЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() ЁЂ
ЁЂ![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌЁЯEOC=90ЁуЃЌ
ЃЌЁЯEOC=90ЁуЃЌ![]() ЪЧ
ЪЧ![]() ЕФНЧЦНЗжЯпЃЌ
ЕФНЧЦНЗжЯпЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЎЦфжавЛжжНтЬтЙ§ГЬШчЯТЃКЧыдкРЈКХжазЂУїИљОнЃЌдкКсЯпЩЯВЙШЋВНжшЃЎ
ЕФЖШЪ§ЃЎЦфжавЛжжНтЬтЙ§ГЬШчЯТЃКЧыдкРЈКХжазЂУїИљОнЃЌдкКсЯпЩЯВЙШЋВНжшЃЎ
НтЃКЁп![]()
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
Ёр![]()
![]()
Ёп![]() ЪЧ
ЪЧ![]() ЕФНЧЦНЗжЯп
ЕФНЧЦНЗжЯп
Ёр![]()
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
Ёр![]()
![]()
Ёп![]()
![]()
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
Ёр![]()
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
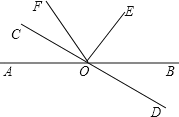
ЁОЬтФПЁПШчЭМЃЌЁЯAOB=ЁЯDOC=90ЁуЃЌOEЦНЗжЁЯAODЃЌЗДЯђбгГЄЩфЯпOEжСF.
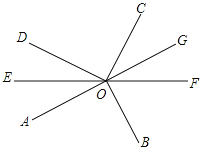
ЃЈ1ЃЉЁЯAODКЭЁЯBOCЪЧЗёЛЅВЙЃПЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЩфЯпOFЪЧЁЯBOCЕФЦНЗжЯпТ№ЃПЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЗДЯђбгГЄЩфЯпOAжСЕуGЃЌЩфЯпOGНЋЁЯCOFЗжГЩСЫ4ЃК3ЕФСНИіНЧЃЌЧѓЁЯAOD.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ4ЕФе§ЗНаЮABCDжаЃЌPЪЧBCБпЩЯвЛЖЏЕуЃЈВЛКЌBЁЂCЕуЃЉЃЎНЋЁїABPбижБЯпAPЗелЃЌЕуBТфдкЕуEДІЃЛдкCDЩЯгавЛЕуMЃЌЪЙЕУНЋЁїCMPбижБЯпMPЗелКѓЃЌЕуCТфдкжБЯпPEЩЯЕФЕуFДІЃЌжБЯпPEНЛCDгкЕуNЃЌСЌНгMAЃЌNAЃЎдђвдЯТНсТлжае§ШЗЕФга_____________ЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉЃЎ
ЂйЁЯN\AFЃН45ЁуЃЛЂкЕБPЮЊ BCжаЕуЪБЃЌAEЮЊЯпЖЮNPЕФжаДЙЯпЃЛ
ЂлЫФБпаЮAMCBЕФУцЛ§зюДѓжЕЮЊ10ЃЛ ЂмЯпЖЮAMЕФзюаЁжЕЮЊ2![]() ЃЛ
ЃЛ
ЂнЕБЁїABPЁеЁїADNЪБЃЌBPЃН4![]() -4ЃЎ
-4ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com