
����Ŀ����ͼ1����������A��B�����Ӧ�����ֱ���6����6����DCE��90����C��O�غϣ�D����������������ϣ���
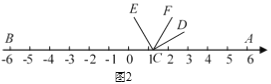
��1����ͼ2������DCE�����������������ƽ��t��0��t��3������λ�����Ƶ㶥��C��ʱ����ת30t�ȣ���CFƽ�֡�ACE����ʱ�ǡ�DCF������
�ٵ�t��1ʱ�������Ķ�����
�ڲ����BCE������������ϵ����֤����
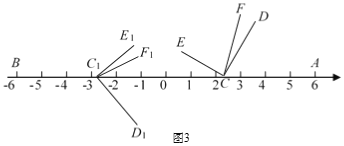
��2����ͼ3����ʼ��D1C1E1���DCE�غϣ�����DCE�����������������ƽ��t��0��t��3������λ�����Ƶ㶥��C��ʱ����ת30t�ȣ���CFƽ�֡�ACE����ʱ�ǡ�DCF���������ͬʱ������D1C1E1������ĸ���������ƽ��t��0��t��3������λ�����Ƶ㶥��C1˳ʱ����ת30t�ȣ���C1F1ƽ�֡�AC1E1���ǡ�D1C1F1������������������![]() �������ʱt��ֵ��
�������ʱt��ֵ��
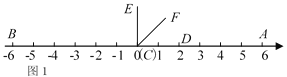
���𰸡���1��������30�����ڡ�BCE��2�������ɼ���������2��t��![]() ��
��
��������
��1������![]() ���������30���������ý�ƽ���ߵ��������
���������30���������ý�ƽ���ߵ��������![]() ������2����������ϵ��
������2����������ϵ��
��2���ɣ�1���ķ�����t�Ĺ�ϵʽ��ʾ����������Ȼ�����![]() �г����̣����t��ֵ��
�г����̣����t��ֵ��
�⣺��1���ٵ�t��1ʱ��
�ߡ�DCA��30������ECD��90����
���ECA��120����
��CFƽ�֡�ACE��
���FCA��![]() ��ECA��60��
��ECA��60��
��������FCD��60����30����30��
����ͼ2�У����룺��BCE��2����
���ɣ��ߡ�DCE��90������DCF������
���ECF��90��������
��CFƽ�֡�ACE��
���ACF����ECF��90��������
�ߵ�A��O��B����
���AOB��180��
���BCE����AOB����ECD����ACD��180����90������90����2������2����
��2����ͼ3�У������⣺������FCA����DCA��![]() ��90��+30t����30t��45����15t��
��90��+30t����30t��45����15t��
������AC1D1+��AC1F1��30t+![]() ��90����30t����45��+15t��
��90����30t����45��+15t��
��|������|��15����
��|30t|��15����
���t��![]() ��
��


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�

��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��֤���е��ı���EFGH��ƽ���ı��Σ�
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90�㣬�����������䣬ֱ��д���е��ı���EFGH����״��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ�ַdz���Ҫ����ѧ���������һ�����ṩ����֪�����а���������������ǿ��Է������������⣮���磺��|x|=2��|y|=3��x+y��ֵ��
�������x=2��y=3ʱ��x+y=5
�������x=2��y=��3ʱ��x+y=��1
�������x=��2��y=3ʱ��x+y=1
�������x=��2��y=��3ʱ��x+y=��5
���ԣ�x+y��ֵΪ1����1��5����5��
���ε�ѧϰ������Ҳ�����Ƶ������
���⣨1������֪��A��B��C��һ��ֱ���ϣ���AB=8��BC=3����AC��Ϊ���٣�
ͨ���������Ƿ��֣�������������������
���������C�ڵ�B���Ҳ�ʱ����ͼ1����ʱ��AC=�� ��
���������C�ڵ�B�����ʱ����ͼ2����ʱ��AC=�� ��
ͨ���������⣬���Ƿ��֣�������ͼ���������Ǹ��õĽ��з��࣮
���⣨2������ͼ3�������ϵ�A�͵�B��ʾ�����ֱ��ǩ�1��2����C��������һ�㣬��BC=2AB�����C��ʾ�����Ƕ��٣�
��������1������ͼ�Σ����ͼ��д��������ͽ����
���⣨3������O��ֱ��AB��һ�㣬��OΪ�˵�������OC��OD��ʹ��AOC=60�㣬OCOD������BOD�Ķ���������ͼ�Σ�ֱ��д�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Խ��Խ������Ǽ��뵽ȫ�������ȳ�����.������������Ϊһ�������ٶȺ��˶�������ɢ���;���֮��IJ����˶������䲻�����˶��˺����������䡢ʱ��ͳ������Ƶ��ŵ���ܵ����ǵ�ϲ��.������Ϣ�����ķ�չ���ܶ��ֻ�![]() ���Լ�¼����ÿ�콡���ߵIJ�����Ϊ��ҵĽ������ü�¼.
���Լ�¼����ÿ�콡���ߵIJ�����Ϊ��ҵĽ������ü�¼.
С���İְ����趼�ǽ����߰����ߣ�һ������£�����ÿ�춼���ֽ�����.С��Ϊ�˸��ְ�����䷢4�·ݵ����˶����������£������˳������飬�������£��벹������.
��4�·������ȡ10�죬��¼�ְ������˶�������ǧ�������£�
�ְ�12 10 11 15 14 13 14 11 14 12
����11 14 15 2 11 11 14 15 14 14
����������Ϣ�����������������±���ʾ��
ƽ���� | ��λ�� | ���� | |
�ְ� | 12.6 | 12.5 |
|
���� |
| 14 | 14 |
��1��ֱ��������հ״�д��������![]() ��
��![]() ��ֵ��
��ֵ��
��2������ΪС�����4�·ݵ����˶����������°䷢��˭����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
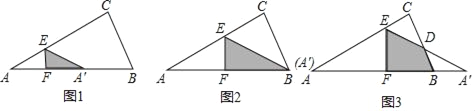
����Ŀ����֪����ͼ1����ABC�У�AB=6��AC=![]() ��BC=3������AC�ϵĶ���E����E�����A��C�غϣ���EF��AB�ڵ�F������AEF��EF���ڵ�ֱ���۵��õ���A'EF����CE=x���۵������A'EF���ı���BCEF�ص����ֵ������ΪS��
��BC=3������AC�ϵĶ���E����E�����A��C�غϣ���EF��AB�ڵ�F������AEF��EF���ڵ�ֱ���۵��õ���A'EF����CE=x���۵������A'EF���ı���BCEF�ص����ֵ������ΪS��
��1����ͼ2������A'�붥��B�غ�ʱ����AE�ij���
��2����ͼ3������A'������ABC���ⲿʱ��A'E��BC�ཻ�ڵ�D����֤����A'BD�ǵ��������Σ�
��3�����ú�x��ʽ�ӱ�ʾS������S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
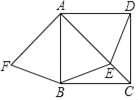
����Ŀ����ͼ��������ABCD������E��AC�ϣ�AF��AC������ΪA��AF��AE��
��1��BF��DE��������������ϵ����֤����Ľ��ۣ�
��2�����������������ֲ����������£�����E�˶���AC�е�ʱ���ı���AFBE��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˹��������Լ��ˮ�����÷ֽμƷѵķ������¼���ÿ����ͥ��ˮ��:����ˮ��������![]() ʱ����
ʱ����![]() ���㣬����ˮ������
���㣬����ˮ������![]() ʱ�����е�
ʱ�����е�![]() ��
��![]() Ԫ/
Ԫ/![]() ���㣬�������ְ�
���㣬�������ְ�![]() Ԫ/
Ԫ/![]() ����.��ij����ͥ����ˮ��
����.��ij����ͥ����ˮ��![]() .
.
(1)�ú�![]() ��ʽ�ӱ�ʾ:
��ʽ�ӱ�ʾ:
��![]() ʱ��ˮ��Ϊ Ԫ;��
ʱ��ˮ��Ϊ Ԫ;��![]() ʱ��ˮ��Ϊ Ԫ;
ʱ��ˮ��Ϊ Ԫ;
(2)
�·� | 4�� | 5�� | 6�� |
��ˮ�� |
|
|
|
С���ҵڶ�������ˮ������ϱ���С����������ȹ�����ˮ��![]() Ԫ���������С����
Ԫ���������С����![]() �·���ˮ��
�·���ˮ��![]() ��ֵ?
��ֵ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
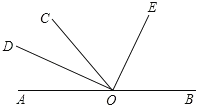
����Ŀ����ͼ��OΪֱ��AB��һ�㣬��AOC=50�㣬ODƽ�֡�AOC����DOE=90�㣮
��1��д��ͼ��С��ƽ�ǵĽǣ�
��2�������BOD�Ķ�����
��3��С������OEƽ�֡�BOC������ͨ������˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
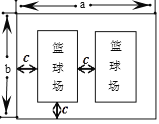
����Ŀ���������ijУ�Բٳ�������ά���죬��ͼ�Dzٳ���һ��.�ڳ�Ϊ![]() �ף���Ϊ
�ף���Ϊ![]() �ij����γ����м䣬������������С��ͬ����������������֮���Լ������볤���γ��ر��صľ��붼Ϊ
�ij����γ����м䣬������������С��ͬ����������������֮���Լ������볤���γ��ر��صľ��붼Ϊ![]() ��.
��.
(1)ֱ��д��һ�����ij��Ϳ���(�ú���ĸ![]() ��
��![]() ��
��![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
(2)�ú���ĸ![]() ��
��![]() ��
��![]() �Ĵ���ʽ��ʾ����������ռ������ĺͣ��������
�Ĵ���ʽ��ʾ����������ռ������ĺͣ��������![]() ��
��![]() ��
��![]() ʱ������������ռ������ĺ�.
ʱ������������ռ������ĺ�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com