
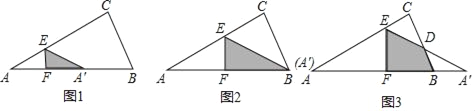
【题目】已知:如图1,△ABC中,AB=6,AC=![]() ,BC=3,过边AC上的动点E(点E不与点A、C重合)作EF⊥AB于点F,将△AEF沿EF所在的直线折叠得到△A'EF,设CE=x,折叠后的△A'EF与四边形BCEF重叠部分的面积记为S.
,BC=3,过边AC上的动点E(点E不与点A、C重合)作EF⊥AB于点F,将△AEF沿EF所在的直线折叠得到△A'EF,设CE=x,折叠后的△A'EF与四边形BCEF重叠部分的面积记为S.
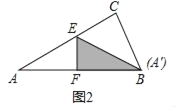
(1)如图2,当点A'与顶点B重合时,求AE的长;
(2)如图3,当点A'落在△ABC的外部时,A'E与BC相交于点D,求证:△A'BD是等腰三角形;
(3)试用含x的式子表示S,并求S的最大值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)首先证明∠A=30°,在Rt△AEF中,解直角三角形即可解决问题;
(2)想办法证明∠A′=∠A′DB=30°,可得BD=BA′;
(3)分两种情形分别求解,①如图3中,当0<x≤![]() 时,重叠部分是四边形EFBD.②如图1中,
时,重叠部分是四边形EFBD.②如图1中,![]() <x<3
<x<3![]() 时,重叠部分是△EFA′;
时,重叠部分是△EFA′;
(1)如图2中,
∵AC2+BC2=(3![]() )2+32=36,AB2=36,
)2+32=36,AB2=36,
∴△ABC是直角三角形,∠C=90°,
当点A'与顶点B重合时,AF=FB=3,
cosA=![]() ,
,
∴∠A=30°,
∴AE=![]() .
.
(2)如图3中,
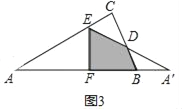
由(1)可知∠A=30°,∠C=90°,
∴∠ABC=60°,
∵∠ABC=∠A′+∠BDA′,∠A′=∠A=30°,
∴∠A′=∠A′DB=30°,
∴BD=BA′,
∴△BDA′是等腰三角形.
(3)①如图3中,当0<x≤![]() 时,重叠部分是四边形EFBD,
时,重叠部分是四边形EFBD,
S=S△EFA′﹣S△BDA′
=![]()
![]() (3
(3![]() ﹣x)
﹣x)![]() (3
(3![]() ﹣x)﹣
﹣x)﹣![]() [
[![]() (3
(3![]() ﹣x)﹣6]×
﹣x)﹣6]×![]() [
[![]() (3
(3![]() ﹣x)﹣6]
﹣x)﹣6]
=﹣![]()
∴S最大值=
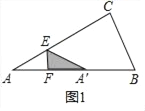
②如图1中,![]() <x<3
<x<3![]() 时,重叠部分是△EFA′,
时,重叠部分是△EFA′,
S=![]() (x﹣3
(x﹣3![]() )2,
)2,
S最大值=3![]() ,
,
3![]() <
<![]() ,
,
∴S的最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
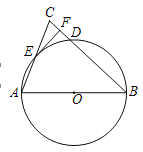
【题目】已知:在△ABC中,AB=BC,以AB为直径作![]() ,交BC于点D,交AC于E,过点E作
,交BC于点D,交AC于E,过点E作![]() 切线EF,交BC于F.
切线EF,交BC于F.
(1)求证:EF⊥BC;
(2)若CD=2,tanC=2,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎做一道数学题,“已知两个多项式![]() ,
,![]() ,试求
,试求![]() .”其中多项式
.”其中多项式![]() 的二次项系数印刷不清楚.
的二次项系数印刷不清楚.
(1)小马虎看答案以后知道![]() ,请你替小马虎求出系数“
,请你替小马虎求出系数“![]() ”;
”;
(2)在(1)的基础上,小马虎已经将多项式![]() 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式![]() ,要求小马虎求出
,要求小马虎求出![]() 的结果.小马虎在求解时,误把“
的结果.小马虎在求解时,误把“![]() ”看成“
”看成“![]() ”,结果求出的答案为
”,结果求出的答案为![]() .请你替小马虎求出“
.请你替小马虎求出“![]() ”的正确答案.
”的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售量 | 销售收入 | |
A型号 | B型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在数轴上A、B两点对应的数分别是6、﹣6,∠DCE=90°(C与O重合,D点在数轴的正半轴上).
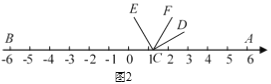
(1)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
①当t=1时,求α的度数;
②猜想∠BCE和α的数量关系,并证明;
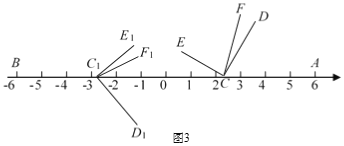
(2)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足![]() ,求出此时t的值.
,求出此时t的值.
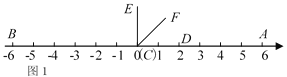
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
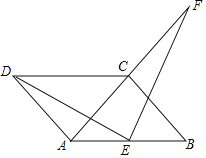
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
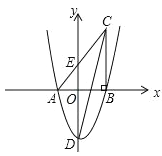
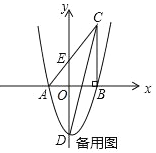
【题目】如图,在平面直角坐标系中,△ABC 的一边 AB 在 x 轴上,∠ABC=90°,点 C(4,8) 在第一象限内,AC 与 y 轴交于点 E,抛物线 y=![]() +bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
+bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
(1)请直接写出抛物线的表达式;
(2)求 ED 的长;
(3)若点 M 是 x 轴上一点(不与点 A 重合),抛物线上是否存在点 N,使∠CAN=∠MAN.若存在,请直接写出点 N 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
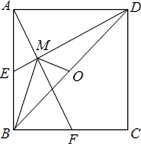
【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com