
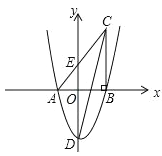
【题目】如图,在平面直角坐标系中,△ABC 的一边 AB 在 x 轴上,∠ABC=90°,点 C(4,8) 在第一象限内,AC 与 y 轴交于点 E,抛物线 y=![]() +bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
+bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
(1)请直接写出抛物线的表达式;
(2)求 ED 的长;
(3)若点 M 是 x 轴上一点(不与点 A 重合),抛物线上是否存在点 N,使∠CAN=∠MAN.若存在,请直接写出点 N 的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x﹣6;(2)
x﹣6;(2)![]() ;(3) S=﹣
;(3) S=﹣![]() m2+
m2+![]() m+26(﹣2<m<4);(4)满足条件的N点坐标为(
m+26(﹣2<m<4);(4)满足条件的N点坐标为(![]() ,
,![]() );(
);(![]() ,﹣
,﹣![]() ).
).
【解析】(1)先确定B(4,0),再利用待定系数法求出抛物线解析式为y=![]() x2-
x2-![]() x-6;
x-6;
(2)先利用待定系数法求得直线AC的解析式为y=![]() x+
x+![]() ,则可确定E(0,
,则可确定E(0,![]() ),然后计算DE的长;
),然后计算DE的长;
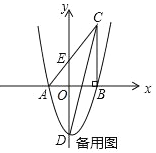
(3)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,根据角平分线的性质得FH=FB,易得AH=AB=6,再利用∠ACB的余弦可求出CF=5,则F(4,3),接着求出直线AF的解析式为y=![]() x+1,于是通过解方程组
x+1,于是通过解方程组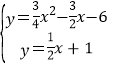 ,得N点坐标为(
,得N点坐标为(![]() ,
,![]() );当点M′在x的负半轴上时,AN′交y轴与G,先在证明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组
);当点M′在x的负半轴上时,AN′交y轴与G,先在证明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组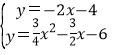 得N′的坐标.
得N′的坐标.
(1)∵BC⊥x轴,点C(4,8),
∴B(4,0),
把B(4,0),C(0,﹣6)代入y=![]() +bx+c得
+bx+c得![]() ,解得
,解得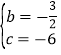 ,
,
∴抛物线解析式为y=![]() x﹣6;
x﹣6;
(2)设直线AC的解析式为y=px+q,
把A(﹣2,0),C(4,8)代入得![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为y=![]() x+
x+![]() ,
,
当x=0时,y=![]() x+
x+![]() =
=![]() ,则E(0,
,则E(0,![]() ),
),
∴DE=![]() +6=
+6=![]() ;
;
(3)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,
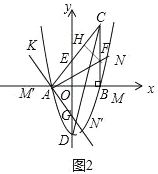
则FH=FB,
易得AH=AB=6,
∵AC=![]() ,
,
∴CH=10﹣6=4,
∵cos∠ACB=![]() ,
,
∴CF=![]() ,
,
∴F(4,3),
易得直线AF的解析式为y=![]() x+1,
x+1,
解方程组 得
得![]() 或
或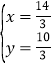 ,
,
∴N点坐标为(![]() ,
,![]() );
);
当点M′在x的负半轴上时,AN′交y轴与G,
∵∠CAN′=∠M′AN′,
∴∠KAM′=∠CAK,
而∠CAN=∠MAN,
∴∠KAC+∠CAN=90°,
而∠MAN+∠AFB=90°,
∴∠KAC=∠AFB,
而∠KAM′=∠GAO,
∴∠GAO=∠AFB,
∴Rt△OAG∽Rt△BFA,
∴![]() ,即
,即![]() ,解得OG=4,
,解得OG=4,
∴G(0,﹣4),
易得直线AG的解析式为y=﹣2x﹣4,
解方程组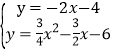 得
得![]() 或
或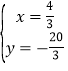 ,
,
∴N′的坐标为(![]() ,﹣
,﹣![]() ),
),
综上所述,满足条件的N点坐标为(![]() ,
,![]() );(
);(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
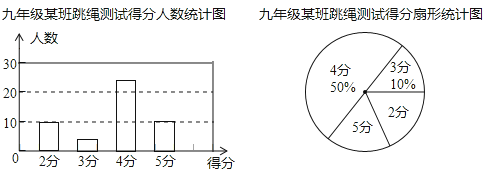
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行了第二次测试,测得成绩的最低分为3分.且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
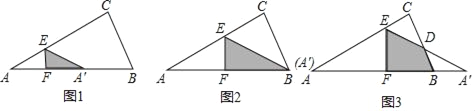
【题目】已知:如图1,△ABC中,AB=6,AC=![]() ,BC=3,过边AC上的动点E(点E不与点A、C重合)作EF⊥AB于点F,将△AEF沿EF所在的直线折叠得到△A'EF,设CE=x,折叠后的△A'EF与四边形BCEF重叠部分的面积记为S.
,BC=3,过边AC上的动点E(点E不与点A、C重合)作EF⊥AB于点F,将△AEF沿EF所在的直线折叠得到△A'EF,设CE=x,折叠后的△A'EF与四边形BCEF重叠部分的面积记为S.
(1)如图2,当点A'与顶点B重合时,求AE的长;
(2)如图3,当点A'落在△ABC的外部时,A'E与BC相交于点D,求证:△A'BD是等腰三角形;
(3)试用含x的式子表示S,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过![]() 时,按
时,按![]() 计算,月用水量超过
计算,月用水量超过![]() 时,其中的
时,其中的![]() 仍按
仍按![]() 元/
元/![]() 计算,超过部分按
计算,超过部分按![]() 元/
元/![]() 计算.设某户家庭月用水量
计算.设某户家庭月用水量![]() .
.
(1)用含![]() 的式子表示:
的式子表示:
当![]() 时,水费为 元;当
时,水费为 元;当![]() 时,水费为 元;
时,水费为 元;
(2)
月份 | 4月 | 5月 | 6月 |
用水量 |
|
|
|
小花家第二季度用水情况如上表,小花家这个季度共缴纳水费![]() 元,请你求出小花家
元,请你求出小花家![]() 月份用水量
月份用水量![]() 的值?
的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
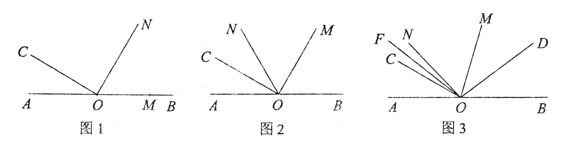
【题目】如图1, 点![]() 在直线
在直线![]() 上,
上,![]() ,将.
,将.![]() 绕着点
绕着点![]() 以
以![]() 的速度逆时针旋转,设旋转时间为
的速度逆时针旋转,设旋转时间为![]() .
.
(1)如图2,当![]() 平分
平分![]() 时,
时,![]() ______
______![]() ; 图中
; 图中![]() 的补角有: ______;
的补角有: ______;
(2)如图3,当![]() 时,
时,![]() 平分
平分![]() ,
, ![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
(3)在![]() 绕着点
绕着点![]() 逆时针旋转的过程中,当
逆时针旋转的过程中,当![]() ______
______![]() 时,
时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
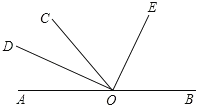
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)写出图中小于平角的角.
(2)求出∠BOD的度数.
(3)小明发现OE平分∠BOC,请你通过计算说明道理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农科所向农民推荐渝江Ⅰ号和渝江Ⅱ号两种新型良种稻谷.在田间管理和土质相同的条件下,Ⅱ号稻谷单位面积的产量比Ⅰ号稻谷低20%,但Ⅱ号稻谷的米质好,价格比Ⅰ号高.已知Ⅰ号稻谷国家的收购价是1.6元/千克.
(1)当Ⅱ号稻谷的国家收购价是多少时,在田间管理、土质和面积相同的两块田里分别种植Ⅰ号、Ⅱ号稻谷的收益相同?
(2)去年小王在土质、面积相同的两块田里分别种植Ⅰ号、Ⅱ号稻谷,且进行了相同的田间管理.收获后,小王把稻谷全部卖给国家.卖给国家时,Ⅱ号稻谷的国家收购价定为2.2元/千克,Ⅰ号稻谷国家的收购价未变,这样小王卖Ⅱ号稻谷比卖Ⅰ号稻谷多收入1040元,那么小王去年卖给国家的稻谷共有多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级两个班,各选派10名学生参加学校举行的“建模”大赛预赛,各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 |
| 93 | 93 | 12 |
八(2)班 | 99 | 95 |
|
| 8.4 |
(1)直接写出表中![]() 、
、![]() 、
、![]() 的值为:
的值为:![]() _____,
_____,![]() _____,
_____,![]() _____;
_____;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好.”但也有人说(2)班的成绩要好.请给出两条支持八(2)班成绩好的理由;
(3)学校从平均数、中位数、众数、方差中选取确定了一个成绩,等于或大于这个成绩的学生被评定为“优秀”等级,如果八(2)班有一半的学生能够达到“优秀”等级,认为这个成绩应定为_____分.
查看答案和解析>>
科目:初中数学 来源: 题型:
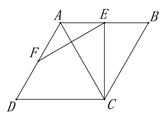
【题目】如图,四边形ABCD是边长为2的菱形,E,F分别是AB,AD的中点,连接EF,EC,将△FAE绕点F旋转180°得到△FDM.
(1)补全图形并证明:EF⊥AC;
(2)若∠B=60°,求△EMC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com