
【题目】如图,在△ABC中,∠C=90°,∠B=30°
(1)在BC上作出点D,使它到A,B两点的距离相等(用尺规作图法,保留作图痕迹,不要求写作法)
(2)若BD=6,求CD长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
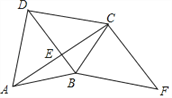
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
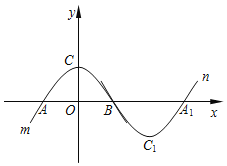
【题目】如图所示,抛物线m:![]() 与x轴于点A、
与x轴于点A、![]() 点A在点B的左侧
点A在点B的左侧![]() ,与y轴交于点
,与y轴交于点![]() 将抛物线m绕点B旋转
将抛物线m绕点B旋转![]() ,得到新的抛物线n,它的顶点为
,得到新的抛物线n,它的顶点为![]() ,与x轴的另一个交点为
,与x轴的另一个交点为![]() .
.
![]() 当
当![]() ,
,![]() 时,求抛物线n的解析式;
时,求抛物线n的解析式;
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 当
当![]() 时,四边形
时,四边形![]() 可能是矩形吗?若能,请求出抛物线m的解析式;若不能,请说明理由.
可能是矩形吗?若能,请求出抛物线m的解析式;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 交于A,B两点,交x轴于D,C两点,已知
交于A,B两点,交x轴于D,C两点,已知![]() ,
,![]() .
.
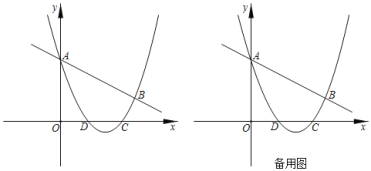
![]() 求抛物线的函数表达式并写出抛物线的对称轴;
求抛物线的函数表达式并写出抛物线的对称轴;
![]() 在直线AB下方的抛物线上是否存在一点E,使得
在直线AB下方的抛物线上是否存在一点E,使得![]() 的面积最大?如果存在,求出E点坐标;如果不存在,请说明理由.
的面积最大?如果存在,求出E点坐标;如果不存在,请说明理由.
![]() 为抛物线上一动点,连接PA,过点P作
为抛物线上一动点,连接PA,过点P作![]() 交y轴于点Q,问:是否存在点P,使得以A、P、Q为顶点的三角形与
交y轴于点Q,问:是否存在点P,使得以A、P、Q为顶点的三角形与![]() 相似?若存在,请直接写出所有符合条件的P点的坐标;若不存在,请说明理由.
相似?若存在,请直接写出所有符合条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
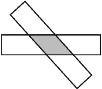
【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )
A. 8B. 10C. 10.4D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是( )

A. 10B. 12C. 20D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
(1)拼成的正方形的面积是 ,边长是 .
(2)把10个小正方形组成的图形纸(如图2),剪开并拼成正方形.
①请在4×4方格图内画出这个正方形.
②以小正方形的边长为单位长度画一条数轴,并在数轴上画出表示-![]() 的点.
的点.
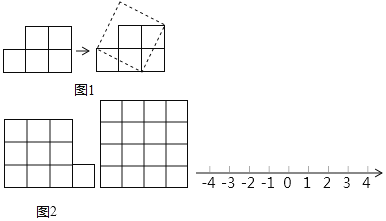
(3)这种研究和解决问题的方式,主要体现了 的数学思想方法.
A.数形结合 B.代入 C.换元 D.归纳
查看答案和解析>>
科目:初中数学 来源: 题型:
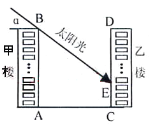
【题目】下图为某小区的两幢1O层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h,太阳光线与水平线的夹角为α.
(1)用含α的式子表示h;
(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com