
【题目】已知:如图,在菱形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为边
为边![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),
不重合),![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,联结
,联结![]() 交对角线
交对角线![]() 于点
于点![]() .设
.设![]() ,
,![]() .
.

(1)求证:![]() 是等边三角形;
是等边三角形;
(2)求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)点![]() 是线段
是线段![]() 的中点,联结
的中点,联结![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)见解析;(2)y=![]() (0<x<2);(3)
(0<x<2);(3)![]() .
.
【解析】
(1)首先由△ABC是等边三角形,即可得AB=AC,求得∠ACF=∠B=60°,然后利由∠BAC=∠EAF=60°,可证明∠BAE=∠CAF,从而可证得△AEB≌△AFC,即可得AE=AF,证得△AEF是等边三角形;
(2)过点E作EH⊥AC于点H,过点F作FM⊥AC于点M,先用含x的代数式表示出HM,然后证明△EGH∽△FGM,得出![]() ,从而可用含x的代数式表示出HG,最后在Rt△EHG中,利用勾股定理可得出x,y之间的关系;
,从而可用含x的代数式表示出HG,最后在Rt△EHG中,利用勾股定理可得出x,y之间的关系;
(3)先用含x的代数式表示出CG的长,然后证明△COE∽△CGF,得出![]() ,从而可得出关于x的方程,解出x的值即可.
,从而可得出关于x的方程,解出x的值即可.
(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ACD都是等边三角形,
∴AB=AC,∠B=∠ACF=60°,
∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF,
∴△BAE≌△CAF(ASA),
∴AE=AF,又∠EAF=60°,
∴△AEF为等边三角形.
(2)解:过点E作EH⊥AC于点H,过点F作FM⊥AC于点M,
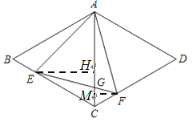
∵∠ECH=60°,∴CH=![]() ,EH=
,EH=![]() x,
x,
∵∠FCM=60°,由(1)知,CF=BE=2-x,∴CM=![]() (2-x),FM=
(2-x),FM=![]() (2-x),
(2-x),
∴HM=CH-CM=![]() -
-![]() (2-x)=x-1.
(2-x)=x-1.
∵∠EHG=∠FMG=90°,∠EGH=∠FGM,
∴△EGH∽△FGM,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴HG=
,∴HG=![]() .
.
在Rt△EHG中,EG2=EH2+HG2,
∴y2=(![]() x)2+[
x)2+[![]() ]2,∴y2=
]2,∴y2=![]() ,∴y=
,∴y=![]() (舍去负值),
(舍去负值),
故y关于x的解析式为y=![]() (0<x<2).
(0<x<2).
(3)解:如图,
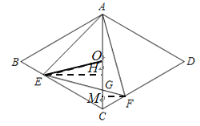
∵O为AC的中点,∴CO=![]() AC=1.
AC=1.
∵EO=EG,EH⊥OC,∴OH=GH,∠EOG=∠EGO,∴∠CGF=∠EOG.
∵∠ECG=60°,EC=x,∴CH=![]() ,∴OH=GH=OC-CH=1-
,∴OH=GH=OC-CH=1-![]() ,∴OG=2OH=2-x,
,∴OG=2OH=2-x,
∴CG=OC-OG=x-1.
∵∠CGF=∠EOC,∠ECO=∠GCF=60°,
∴△COE∽△CGF,
∴![]() ,∴
,∴![]() ,整理得x2=2,
,整理得x2=2,
∴x=![]() (舍去负值),经检验x是原方程的解.
(舍去负值),经检验x是原方程的解.
故x的值为![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
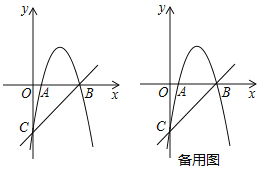
(1)求抛物线的解析式;
(2)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() .
.
①当![]() 时,过抛物线上一动点
时,过抛物线上一动点![]() (不与点
(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标;
的横坐标;
②连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() 的
的![]() 倍时,请直接写出点
倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D是AB延长线上的一点,点C在⊙O上,且AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,求图中阴影部分的面积.
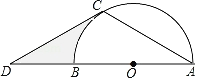
查看答案和解析>>
科目:初中数学 来源: 题型:
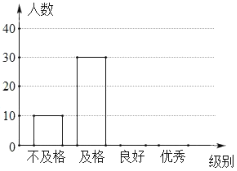
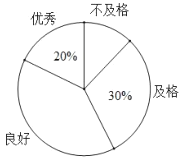
【题目】新冠肺炎疫情发生以来,专家给出了很多预防建议.为普及预防措施,某校组织了由八年级800名学生参加的“防新冠”知识竞赛.李老师为了了解学生的答题情况,从中随机抽取了部分同学的成绩作为样本,把成绩按优秀、良好、及格、不及格4个级别进行统计,并绘制成了如图的条形统计图和扇形统计图(部分信息未给出).
请根据以上提供的信息,解答下列问题:
(1)求被抽取的部分学生的人数;
(2)请补全条形统计图;
(3)求出扇形统计图中表示良好级别的扇形的圆心角度数;
(4)请估计八年级的800名学生中达到良好和优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,点O在BC上,以线段OC的长为半径的⊙O与AB相切于点D,分别交BC、AC于点E、F,连接ED并延长,交CA的延长线于点G.
(1)求证:∠DOC=2∠G.
(2)已知⊙O的半径为3.
①若BE=2,则DA= .
②当BE= 时,四边形DOCF为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
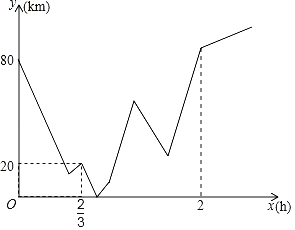
【题目】A、B两地之间有一修理厂C,一日小海和王陆分别从A、B两地同时出发相向而行,王陆开车,小海骑摩托.二人相遇时小海的摩托车突然出故障无法前行,王陆决定将小海和摩托车一起送回到修理厂C后再继续按原路前行,王陆到达A地后立即返回B地,到B地后不再继续前行,等待小海前来(装载摩托车时间和掉头时间忽略不计),整个行驶过程中王陆速度不变,而小海在修理厂花了十分钟修好摩托车,为了赶时间,提速![]() 前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com