
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.
如:![]() ,
,![]() ,
,![]() ,因此
,因此![]() ,
,![]() ,
,![]() 这三个数都是神秘数.
这三个数都是神秘数.
(1)![]() 是神秘数吗?为什么?
是神秘数吗?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 取非负整数),由这两个连续偶数构造的神秘数是
取非负整数),由这两个连续偶数构造的神秘数是![]() 的倍数吗?为什么?
的倍数吗?为什么?
(3)①若长方形相邻两边长为两个连续偶数,试说明其周长一定为神秘数.
②在①的条件下,面积是否为神秘数?为什么?
【答案】(1)是,见详解;(2)是,见详解;(3)①见详解,②是,见详解
【解析】
(1)根据“神秘数”的定义,只需看能否把28这个数写成两个连续偶数的平方差即可判断;
(2)运用平方差公式进行计算,进而判断即可;
(3)①运用周长公式进行计算,进而判断即可,②运用面积公式进行计算,进而判断即可.
解:(1)28是“神秘数”,理由如下:
∵28=82-62,能表示为两个连续偶数的平方差,
∴28是“神秘数”;
(2)“神秘数”是4的倍数.理由如下:
∵(2k+2)2-(2k)2=(2k+2+2k)(2k+2-2k)=2(4k+2)=4(2k+1),
∴“神秘数”是4的倍数;
(3)①设两个连续的偶数为:2k,2k+2(其中![]() 取非负整数),
取非负整数),
则周长=![]() ,
,
而由(2)知“神秘数”可表示为4(2k+1),
∴长方形相邻两边长为两个连续偶数,则其周长一定为神秘数.
②长方形的面积=![]() ,
,
∵![]() 取非负整数,
取非负整数,
∴在①的条件下,面积是神秘数.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 为
为![]() 直径,
直径,![]() 是直径
是直径![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() ,
,![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 上一点(不与点
上一点(不与点![]() ,
,![]() 重合),且
重合),且![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() .
.
![]() 如图
如图![]() ,当点
,当点![]() 在线段
在线段![]() 上时,试判断
上时,试判断![]() 与
与![]() 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;
![]() 当点
当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,其它条件不变.
时,其它条件不变.

①请你在图![]() 中画出符合要求的图形,并参照图
中画出符合要求的图形,并参照图![]() 标记字母;
标记字母;
②判断![]() 中的结论是否还成立,请说明理由.
中的结论是否还成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=40°,点P在∠AOB的内部,点C,D分别是点P关于直线OA,OB的对称点,连接CD分别交OA,OB于点E、F.则∠EPF=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() ,
,![]() 是对角线.将
是对角线.将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .则下列结论:
.则下列结论:
①四边形![]() 是菱形②
是菱形②![]() ③
③![]()
④![]() ,其中正确的结论是( )
,其中正确的结论是( )

A. ①②③④ B. ①②③ C. ①② D. ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图矩形![]() 的对角线
的对角线![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,判断四边形
,判断四边形![]() 的形状并说明理由.
的形状并说明理由.
(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.
(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角板按图①所示的位置放置,图②是由它抽象画出的几何图形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() .
.
(1)请找出图②中与![]() 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在BC边上,DE垂直平分AC边,垂足为点E,若∠B=70°,且AB+BD=BC,则∠BAC的度数是( )

A.65°B.70°C.75°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图与说理(要求保留作图痕迹,不写作法.)如图,在Rt△ABC中,∠ACB=90°
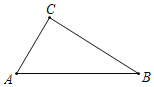
(1)过点C作AB的垂线CD,交AB于点D;
(2)作∠ABC的平分线BE交AC于点E,交CD于点F;
(3)观察线段CE与CF有何数量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com