
定义:如图⑴,若分别以△ABC的三边AC,BC,AB为边向三角形外侧作正方形ACDE,BCFG和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展双叶正方形.
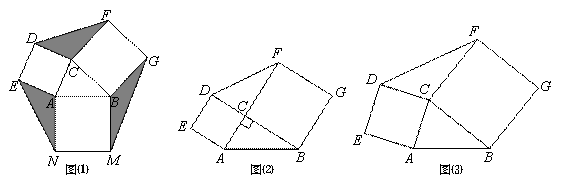 |
(1)作△ABC的外展双叶正方形ACDE和BCFG,记△ABC,△DCF的面积分别为
S1和S2.
① 如图⑵,当∠ACB=90°时,求证:S1=S2.
② 如图⑶,当∠ACB≠90°时,S1与S2是否仍然相等,请说明理由.
(2)已知△ABC中,AC=3,BC=4,作其外展三叶正方形,记△DCF,△AEN,△BGM的面积和为S,请利用图⑴探究:当∠ACB的度数发生变化时,S的值是否发生变化,若不变,求出S的值;若变化,求出S的最大值.
(1)证明:∵正方形ACDE和正方形BCFG,
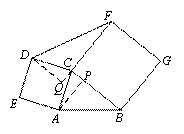 ∴AC=DC,BC=FC,∠ACD=∠BCF=90°,
∴AC=DC,BC=FC,∠ACD=∠BCF=90°,
又∵∠ACB=90°,∴∠DCF=90°,
∴∠ACB=∠DCF=90°,
∴△ABC≌△DFC.
∴S1=S2.
(2) S1=S2.
理由如下:
如图,过点A作AP⊥BC于点P,
过点D作DQ⊥FC交FC的延长线于点Q.
∴∠APC=∠DQC=90°.
∵四边形ACDE,BCFG均为正方形,
∴AC=CD,BC=CF,∠ACP+∠ACQ=90°,∠DCQ+∠ACQ=90°.
∴∠ACP=∠DCQ.
∴△APC ≌△DQC.(AAS)
∴AP=DQ.
又∵S1=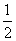 BC•AP,S2=
BC•AP,S2=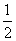 FC•DQ,
FC•DQ,
∴S1=S2..
(3) 由(2)得,S是△ABC面积的三倍,
要使S最大,只需三角形ABC的面积最大,
∴当△ABC是直角三角形,即∠ACB=90°时,S有最大值.
此时,S=3S△ABC=3×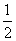 ×3×4=18.
×3×4=18.


科目:初中数学 来源: 题型:
二次函数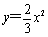 的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数位于第一象限的图象上,点C1,C2,C3,…,Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3,…,四边形An-1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3=…=∠An-1BnAn=60°,则A1点的坐标为 ,菱形An-1BnAnCn的周长为 .
的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数位于第一象限的图象上,点C1,C2,C3,…,Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3,…,四边形An-1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3=…=∠An-1BnAn=60°,则A1点的坐标为 ,菱形An-1BnAnCn的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数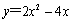 .
.
(1)将此函数解析式用配方法化成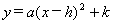 的形式;
的形式;
(2)在给出的直角坐标系中画出此函数的图象(不要求列对应数值表,但要求尽可能画准确);
(3)当0<x<3时,观察图象直接写出函数值y的取值范围: .
查看答案和解析>>
科目:初中数学 来源: 题型:
下列调查中,适宜采用全面调查(普查)方式的是( )
A.某条河流水质情况的调查 B.某品牌烟花爆竹燃放安全情况的调查
C.一批灯管使用寿命的调查 D.对“神舟十号”飞船各零部件合格情况的调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com