
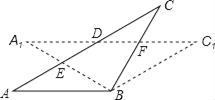
【题目】在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中一定正确的有
A. ①②④ B. ②③④ C. ①②⑤ D. ③④⑤
【答案】C
【解析】
①两个不同的三角形中有两个角相等,那么第三个角也相等;
②根据ASA进而得出△A1BF≌△CBE,即可得出A1E=CF;
③∠CDF=α,而∠C与顺时针旋转的度数不一定相等,所以DF与FC不一定相等;
④AE不一定等于CD,则AD不一定等于CE,
⑤用角角边可证明△A1BF≌△CBE后可得A1F=CE.
∵△ABC绕点B顺时针旋转α度,得到△A1BC1,
∴∠CBC1=α,∠C=∠C1,
∵∠BFC1=∠DFC,
∴∠CDF=∠CBC1=α,故①正确,
∵AB=BC,
∴∠A=∠C,
∴∠C=∠A1
在△A1BF和△CBE中,
∠C=∠A1,A1B=BC,∠A1BF=∠CBE,
∴△A1BF≌△CBE,
∴BE=BF,A1F=CE,故⑤正确,
∵A1B=BC,
∴A1B-BE=BC-BF,即A1E=CF,故②正确,
∵∠CDF=α,α是可变化的角,∠C是固定角,
∴∠CDF不一定等于∠C,
∴DF不一定等于CF,故③错误,
∵AE不一定等于CD,
∴AD不一定等于CE,故④错误.
综上所述:①②⑤正确,
故选C.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.

(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
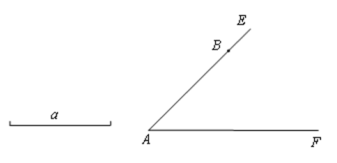
【题目】如图,已知线段a和∠EAF,点B在射线AE上 . 画出△ABC,使点C在射线AF上,且BC=a.
(1)依题意将图补充完整;
(2)如果∠A=45°,AB=![]() ,BC=5,求△ABC的面积 .
,BC=5,求△ABC的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王强与李明两位同学在学习“概率”时,做抛骰子(正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率;
(2)王强说:“根据试验,可知一次试验中出现向上点数为5的概率最大.”李明说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李明说法的对错.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(提出问题)课间,一位同学拿着方格本遇人便问:“如图所示,在边长为1的小正方形组成的网格中,点A、B、C都是格点,如何证明点A、B、C在同一直线上呢?”

(分析问题)一时间,大家议论开了. 同学甲说:“可以利用代数方法,建立平面直角坐标系,利用函数的知识解决”,同学乙说:“也可以利用几何方法…”同学丙说:“我还有其他的几何证法”……
(解决问题)请你用两种方法解决问题
方法一(用代数方法):

方法二(用几何方法):

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,并且AD是⊙O的直径,C是![]() 的中点,AB和DC的延长线交于⊙O外一点E.
的中点,AB和DC的延长线交于⊙O外一点E.
求证:(1)∠EBC=∠D;
(2)BC=EC.

查看答案和解析>>
科目:初中数学 来源: 题型:
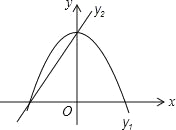
【题目】已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越大;③使得M大于2的x值不存在;④使得M=1的x值是﹣![]() 或
或![]() .其中正确结论的个数为( )
.其中正确结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com