
【题目】如图,已知点D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.

(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
【答案】(1)证明见解析;(2)70°
【解析】
(1)根据AF平分∠DAC得出∠DAF=∠CAF,再根据AF∥BC求得∠DAF=∠B,∠CAF=∠ACB则可证明△ABC是等腰三角形;(2)根据AB=AC,∠B=40°,可求出∠ACE的角度,再根据CG平分∠ACE求出![]() ,则利用AF∥BC求出∠AGC的度数.
,则利用AF∥BC求出∠AGC的度数.
(1)证明:∵AF平分∠DAC,
∴∠DAF=∠CAF,
∵AF∥BC,
∴∠DAF=∠B,∠CAF=∠ACB,
∴∠B=∠ACB,
∴△ABC是等腰三角形;
(2)解:∵AB=AC,∠B=40°,
∴∠ACB=∠B=40°,
∴∠BAC=100°,
∴∠ACE=∠BAC+∠B=140°,
∵CG平分∠ACE,
∴![]() ACE=70°,
ACE=70°,
∵AF∥BC,
∴∠AGC=180°﹣∠BCG=70°.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣3
(1)请你把已知的二次函数化成y=(x﹣h)2+k的形式,并在平面直角坐标系中画出它的图象;
(2)如果A(x1,y1)、B(x2,y2)是(1)中像上的两点,且x1<x2<1,请直接写出y1、y2的大小关系为 .
(3)利用(1)中的图象表示出方程x2﹣2x﹣1=0的根,画在(1)的图象上即可,要求保留画图痕迹.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为_______.
,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 港口位于
港口位于![]() 观测点北偏东
观测点北偏东![]() 方向,且其到
方向,且其到![]() 观测点正北方向的距离
观测点正北方向的距离![]() 的长为
的长为![]() ,一艘货轮从
,一艘货轮从![]() 港口以
港口以![]() 的速度沿如图所示的
的速度沿如图所示的![]() 方向航行,
方向航行,![]() 后达到
后达到![]() 处,现测得
处,现测得![]() 处位于
处位于![]() 观测点北偏东
观测点北偏东![]() 方向,求此时货轮与
方向,求此时货轮与![]() 观测点之间的距离
观测点之间的距离![]() 的长(精确到
的长(精确到![]() ).(参考数据:
).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径
的直径![]() 延长线上的一点,
延长线上的一点,![]() 与
与![]() 相切,切点为
相切,切点为![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() .已知
.已知![]() .下列结论:
.下列结论:
![]() 与
与![]() 相切;
相切;![]() 四边形
四边形![]() 是菱形;
是菱形;![]() ;
;![]() .
.
其中正确的个数为( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC的平分线与∠ACD的平分线交于点A![]() ,∠A
,∠A![]() BC的平分线与∠A
BC的平分线与∠A![]() CD的平分线交于点A
CD的平分线交于点A![]() ,以此类推,∠A
,以此类推,∠A![]() BC的平分线与∠A
BC的平分线与∠A![]() CD的平分线交于点A
CD的平分线交于点A![]() ,则∠A
,则∠A![]() 的大小是___
的大小是___

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 上,将矩形
上,将矩形![]() 沿
沿![]() 折叠压平,使点
折叠压平,使点![]() 落在坐标平面内,设点
落在坐标平面内,设点![]() 的对应点为点
的对应点为点![]() .若抛物线
.若抛物线![]() (
(![]() 且
且![]() 为常数)的顶点落在
为常数)的顶点落在![]() 的内部,则
的内部,则![]() 的取值范围是( )
的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
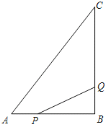
![]() 点
点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() ,
,![]() 同时出发,线段
同时出发,线段![]() 能否将
能否将![]() 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
![]() 若
若![]() 点沿射线
点沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,点
的速度移动,点![]() 沿射线
沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,
的速度移动,![]() 、
、![]() 同时出发,问几秒后,
同时出发,问几秒后,![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
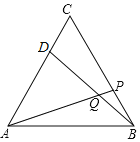
【题目】如图,在等边△ABC的顶点B、C处各有一只蜗牛,它们同时出发,分别都以每分钟1个单位的速度由C向A和由B向C爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、P处,请问:
(1)在爬行过程中,BD和AP始终相等吗?
(2)在爬行过程中BD与AP所成的∠DQA有变化吗?若无变化是多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com