Question

【题目】如图，在等边△ABC的顶点B、C处各有一只蜗牛，它们同时出发，分别都以每分钟1个单位的速度由C向A和由B向C爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t分钟后，它们分别爬行到D、P处，请问：

(1)在爬行过程中，BD和AP始终相等吗？

(2)在爬行过程中BD与AP所成的∠DQA有变化吗？若无变化是多少度？

Answer 1

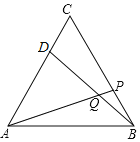
【答案】(1)BD和AP始终相等；(2)∠DQA大小无变化，始终是60°.

【解析】

(1)根据等边三角形性质得出∠CAB＝∠C＝∠ABP＝60°，AB＝BC，根据SAS推出△BDC≌△APB即可.

(2)根据△BDC≌△APB得出∠CBD＝∠BAP，根据三角形外角性质求出∠DQA＝∠ABC，即可求出答案.

解：(1)在爬行过程中，BD和AP始终相等，

理由是：∵△ABC是等边三角形，

∴∠CAB＝∠C＝∠ABP＝60°，AB＝BC，

在△BDC和△APB中，

，

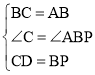∴△BDC≌△APB(SAS)，

∴BD＝AP.

(2)蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化，

理由：∵△BDC≌△APB，

∴∠CBD＝∠BAP，

∴∠DQA＝∠DBA+∠BAP＝∠DBA+∠CBD＝∠ABC＝60°，

即蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化，始终是60°.