
【题目】如图,在△ABC中,∠ACB=![]() ,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
(1)求证:四边形ECBF是平行四边形;
(2) 当∠A=![]() 时,求证:四边形ECBF是菱形.
时,求证:四边形ECBF是菱形.

【答案】(1)详见解析;(2)详见解析.
【解析】
试题(1)根据三角形的中位线定理可得EF∥BC,根据两组对边分别平行的四边形是平行四边形即可判定四边形ECBF是平行四边形;(2)根据直角三角形中30°的锐角所对的直角边等于斜边的一半和斜边的中线等于斜边的一半可得![]() ,
,![]() ,即可得
,即可得![]() ,根据一组邻边相等的平行四边形是菱形即可判定四边形ECBF是菱形.
,根据一组邻边相等的平行四边形是菱形即可判定四边形ECBF是菱形.
试题解析: (1) 证明:∵D,E分别为边AC,AB的中点,
∴DE∥BC,即EF∥BC.
又∵BF∥CE,
∴四边形ECBF是平行四边形.
(2)证法一:
∵∠ACB=![]() ,∠A=
,∠A=![]() ,E为AB的中点,
,E为AB的中点,
∴![]() ,
,![]() .
.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
证法二:
∵∠ACB=![]() ,∠A=
,∠A=![]() ,E为AB的中点,
,E为AB的中点,
∴![]() ,∠ABC=
,∠ABC=![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
证法三:
∵E为AB的中点,∠ACB=![]() ,∠A=
,∠A=![]() ,
,
∴![]() , ∠ABC=
, ∠ABC=![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 上,将矩形
上,将矩形![]() 沿
沿![]() 折叠压平,使点
折叠压平,使点![]() 落在坐标平面内,设点
落在坐标平面内,设点![]() 的对应点为点
的对应点为点![]() .若抛物线
.若抛物线![]() (
(![]() 且
且![]() 为常数)的顶点落在
为常数)的顶点落在![]() 的内部,则
的内部,则![]() 的取值范围是( )
的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.

查看答案和解析>>
科目:初中数学 来源: 题型:
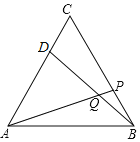
【题目】如图,在等边△ABC的顶点B、C处各有一只蜗牛,它们同时出发,分别都以每分钟1个单位的速度由C向A和由B向C爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、P处,请问:
(1)在爬行过程中,BD和AP始终相等吗?
(2)在爬行过程中BD与AP所成的∠DQA有变化吗?若无变化是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )

A. 24° B. 33° C. 42° D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一透明的口袋中装有![]() 个球,这
个球,这![]() 个球分别标有
个球分别标有![]() ,
,![]() ,
,![]() ,这些球除了数字外都相同.
,这些球除了数字外都相同.
![]() 如果从袋子中任意摸出一个球,那么摸到标有数字是
如果从袋子中任意摸出一个球,那么摸到标有数字是![]() 的球的概率是多少?
的球的概率是多少?
![]() 如果一次摸两个球,用树状图或列表法求出摸到的两个球标有的数字的积为奇数的概率;
如果一次摸两个球,用树状图或列表法求出摸到的两个球标有的数字的积为奇数的概率;
![]() 小明和小亮玩摸球游戏,游戏的规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小亮随机摸出一个球,记下数字.谁摸出的球的数字大,谁获胜.请你用树状图或列表法分析游戏规则对双方是否公平?并说明理由.
小明和小亮玩摸球游戏,游戏的规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小亮随机摸出一个球,记下数字.谁摸出的球的数字大,谁获胜.请你用树状图或列表法分析游戏规则对双方是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购买
份),并规定:顾客每购买![]() 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券![]() 元.
元.

(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费![]() 元,你会选择转转盘还是直接获得购物券?说明理由.
元,你会选择转转盘还是直接获得购物券?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
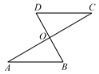
【题目】如图,已知AO=CO,那么添加下列一个条件后,仍无法判定△ABO ≌△CDO 的是( )
A.∠A=∠CB.BO=DOC.AB=CDD.∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距40km,甲、乙两人沿同一路线从A地到B地,甲骑自行车先出发,1.5h后乙乘坐公共汽车出发,两人匀速行驶的路程与时间的关系如图所示.
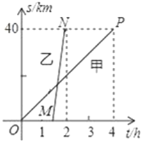
(1)求甲、乙两人的速度;
(2)若乙到达B地后,立即以原速返回A地.
①在图中画出乙返程中距离A地的路程y(km)与时间x(h)的函数图象,并求出此时y与x的函数表达式;
②求甲在离B地多远处与返程中的乙相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com