
【题目】已知![]() 港口位于
港口位于![]() 观测点北偏东
观测点北偏东![]() 方向,且其到
方向,且其到![]() 观测点正北方向的距离
观测点正北方向的距离![]() 的长为
的长为![]() ,一艘货轮从
,一艘货轮从![]() 港口以
港口以![]() 的速度沿如图所示的
的速度沿如图所示的![]() 方向航行,
方向航行,![]() 后达到
后达到![]() 处,现测得
处,现测得![]() 处位于
处位于![]() 观测点北偏东
观测点北偏东![]() 方向,求此时货轮与
方向,求此时货轮与![]() 观测点之间的距离
观测点之间的距离![]() 的长(精确到
的长(精确到![]() ).(参考数据:
).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

【答案】此时货轮与![]() 观测点之间的距离
观测点之间的距离![]() 约为
约为![]() .
.
【解析】
根据在Rt△ADB中,sin∠DBA=![]() ,得出AB的长,进而得出tan∠BAH=
,得出AB的长,进而得出tan∠BAH=![]() ,求出BH的长,即可得出AH以及CH的长,进而得出答案.
,求出BH的长,即可得出AH以及CH的长,进而得出答案.
BC=40×![]() =10,
=10,
在Rt△ADB中,sin∠DBA=![]() ,sin53.2°≈0.8,
,sin53.2°≈0.8,
所以AB=![]() =20,
=20,
如图,过点B作BH⊥AC,交AC的延长线于H,
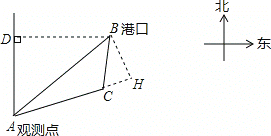
在Rt△AHB中,∠BAH=∠DAC-∠DAB=63.6°-37°=26.6°,
tan∠BAH=![]() ,0.5=
,0.5=![]() ,AH=2BH,
,AH=2BH,
BH2+AH2=AB2,BH2+(2BH)2=202,BH=4![]() ,所以AH=8
,所以AH=8![]() ,
,
在Rt△BCH中,BH2+CH2=BC2,CH=2![]() ,
,
所以AC=AH-CH=8![]() -2
-2![]() =6
=6![]() ≈13.4,
≈13.4,
答:此时货轮与A观测点之间的距离AC约为13.4km.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知a、b都是正整数,且抛物线y=ax2+bx+l与x轴有两个不同的交点A、B.若A、B到原点的距离都小于1,则a+b的最小值等于( )
A. 16 B. 10 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
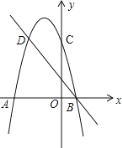
(1)求点D坐标及二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.

(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
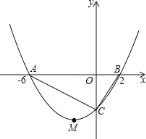
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 能否在抛物线第三象限的图象上找到一点
能否在抛物线第三象限的图象上找到一点![]() ,使
,使![]() 的面积最大?若能,请求出点
的面积最大?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com