【题目】已知a、b都是正整数，且抛物线y=ax2+bx+l与x轴有两个不同的交点A、B．若A、B到原点的距离都小于1，则a+b的最小值等于（ ）
A. 16 B. 10 C. 4 D. 1
【答案】B
【解析】
首先根据a，b都是正整数，得出对称轴的符号，以及△的符号，a-b+c的符号，进而得出不等式组，分析得出a的取值即可．
∵a，b都是正整数，
∴-
＜0，
＞0，
∵抛物线y=ax2+bx+l与x轴有两个不同的交点A、B，
且A、B到原点的距离都小于1，则点A，B两点在0和-1之间，于是，a，b同时满足
，
即
，①
①当
≥b1，即b≤2时，有
≤1，又a＜与a是正整数矛盾，
故＜b-1，即b＞2，若b-1≥，有（b-2）2≤0，则b-1＜，
不等式组①的解为：b-1＜a＜，
若b-1＜a，而a，b都是正整数，取最小的a，令a=b，则
a＜
，
得：a＞4，
取最小的a=5．故a+b的最小值等于10．
故选B．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】转盘被均匀分为37格，分别标以0～36这37个数字，且所有写有偶数(0除外)的格子都涂成了红色，写有奇数的格子都涂成了蓝色，而0所在的格子被涂成了绿色．游戏者用此转盘(如图)做游戏，每次游戏游戏者交游戏费1元，游戏时，游戏者先押一个数字，然后快速地转动转盘，若转盘停止转动时，指针所指格子中的数字恰为游戏者所押数字，则游戏者将获得奖励36元，该游戏对游戏者有利吗？转动多次后，游戏者平均每次将获得或损失多少元？
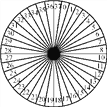
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC是等边三角形.
(1)如图1，点D是边BC的中点，∠ADE＝60°，且DE交△ABC外角∠ACF的平分线CE于点E，求证：AD＝DE；(提示：取AB的中点G，连接DG)
(2)小颖对(1)题进行了探索：如果将(1)题中的“点D是边BC的中点”改为“点D是直线BC上任意一点(B、C两点除外)”，其它条件不变，结论AD＝DE是否仍然成立？小颖将点D的位置分为三种情形，画出了图2、图3、图4，现在请你在图2、图3、图4中选择一种情形，帮小颖验证：结论AD＝DE是否仍然成立？
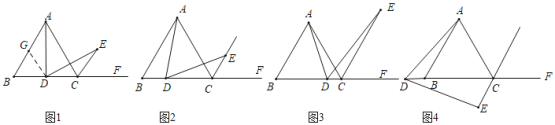
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了实现“畅通市区”的目标，市地铁一号线准备动工，市政府现对地铁一号线第
标段工程进行招标，施工距离全长为
米．经招标协定，该工程由甲、乙两公司承建，甲、乙两公司施工方案及报价分别为：
甲公司施工单价
（万元/米）与施工长度
（米）之间的函数关系为
，
乙公司施工单价
（万元/米）与施工长度（米）之间的函数关系为
．
（注：工程款
施工单价
施工长度）
如果不考虑其他因素，单独由甲公司施工，那么完成此项工程需工程款多少万元？
考虑到设备和技术等因素，甲公司必须邀请乙公司联合施工，共同完成该工程．因设备共享，两公司联合施工时市政府可节省工程款
万元（从工程款中扣除）．
①如果设甲公司施工
米
，那么乙公司施工________米，其施工单价
________万元/米，试求市政府共支付工程款
（万元）与（米）之间的函数关系式；
②如果市政府支付的工程款为
万元，那么应将多长的施工距离安排给乙公司施工？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若a、b、c是△ABC中∠A、∠B、∠C的对边，抛物线y=x2﹣2ax+b2交x轴于M（a+c，0），则△ABC是（ ）
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 不确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=ax2+bx+c的图象如图所示，下列结论正确的是（ ）
①b＜1；②2a+b＞0；③a+c+1＞0；④a﹣b+c＜0；⑤
最大值为3．
A. ②③④⑤ B. ②③④ C. ②③ D. ①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=x2﹣2x﹣3
（1）请你把已知的二次函数化成y=（x﹣h）2+k的形式，并在平面直角坐标系中画出它的图象；
（2）如果A（x1，y1）、B（x2，y2）是（1）中像上的两点，且x1＜x2＜1，请直接写出y1、y2的大小关系为 ．
（3）利用（1）中的图象表示出方程x2﹣2x﹣1=0的根，画在（1）的图象上即可，要求保留画图痕迹．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，
、
两个圆柱形容器放置在同一水平桌面上，开始时容器中盛满水，容器中盛有高度为1 dm的水，容器下方装有一只水龙头，容器向容器匀速注水.设时间为t (s)，容器、中的水位高度
(dm)、
(dm)与时间t (s)之间的部分函数图像如图②所示.根据图中数据解答下列问题:
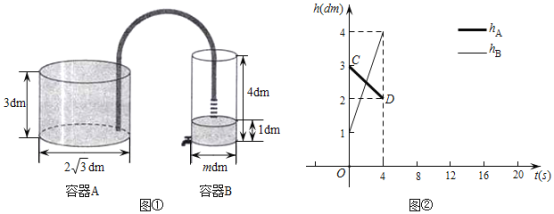
(1)容器向容器注水的速度为 dm3/s(结果保留
)，容器的底面直径
dm;
(2)当容器注满水后，容器停止向容器注水，同时开启容器的水龙头进行放水，放水速度为
dm3/s.请在图②中画出容器中水位高度与时间 (
)的函数图像，说明理由;
(3)当容器B注满水后，容器A继向容器B注水，同时开启容器B的水龙头进行放水，放水速度为
dm3/s，直至容器、水位高度相同时，立即停止放水和注水，求容器向容器全程注水时间.(提示:圆柱体积=圆柱的底面积×圆柱的高)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
港口位于
观测点北偏东
方向，且其到观测点正北方向的距离
的长为
，一艘货轮从港口以
的速度沿如图所示的
方向航行，
后达到
处，现测得处位于观测点北偏东
方向，求此时货轮与观测点之间的距离
的长（精确到
）．（参考数据：
，
，
，
，
，
，
）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com