
【题目】已知抛物线y=ax2+bx+c的图象如图所示,下列结论正确的是( )
①b<1;②2a+b>0;③a+c+1>0;④a﹣b+c<0;⑤![]() 最大值为3.
最大值为3.

A. ②③④⑤ B. ②③④ C. ②③ D. ①②④
【答案】B
【解析】
根据二次函数开口向上判断出a<0,再根据对称轴判断出b>0,再根据与y轴的交点判断出c<0;令x=-1代入抛物线求解即可得到a-b+c=-2,再根据对称轴列出不等式求解即可得到2a+b>0;根据x=-1和x=1时的函数值整理即可求出b>1,根据x=-2,y<0,得出4a-2b+c<0,即可得到a+b+c<3b-3a,进而得出![]() <3.
<3.
①由图可知,x=-1时,y=-2,
所以,a-b+c=-2,
∴c=-2-a+b,
∵x=1时,y>0,
∴a+b+c>0,
∴a+b+(-2-a+b)>0,
∴b>1,
故①不正确;
②∵二次函数开口向下,
∴a<0,
∵对称轴x=1的右边,
∴-![]() >1,
>1,
∴b>-2a,
2a+b>0,
故②正确;
③∵a+b+c>0,
∴a+c>-b,
∴2a+2c>a-b+c,
∵a-b+c=-2,
∴2a+2c>-2,
∴a+c>-1,
∴a+c+1>0;
故③正确;
④由①知:a-b+c=-2,
∴a-b+c<0,
故④正确;
⑤∵当x=-2时,y<0,
∴4a-2b+c<0,
∴a+b+c<3b-3a,
∵b>1,a<0,
∴b-a>0,
∴![]() <3,
<3,
故⑤错误;
综上所述,结论正确的是②③④共3个.
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某中学计划召开“诚信在我心中”主题教育活动,需要选拔活动主持人,经过全校学生投票推荐,有2名男生和1名女生被推荐为候选主持人.
(1)小明认为,如果从3名候选主持人中随机选拔1名,不是男生就是女生,因此选出的主持人是男生和女生的可能性相同,你同意他的说法吗?为什么?
(2)如果从3名候选主持人中随机选拔2名,请通过列表或画树状图求选拔的2名主持人恰好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,网格线的交点称为格点,如图是 3×3 的正方形网格,已知 A,B 是两格点,C是不同于点A和B的格点,下列说法正确的是( ).
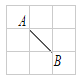
A.ΔABC是直角三角形,这样的点C有4个
B.ΔABC是等腰三角形,这样的点C有4个
C.ΔABC是等腰直角三角形,这样的点C有6个
D.ΔABC是等腰直角三角形,这样的点C有2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,F是AD中点,延长BC到E,CE=![]() BC,连结DE、CF,∠B=60°,AB=3,AD=4,则DE=_______________
BC,连结DE、CF,∠B=60°,AB=3,AD=4,则DE=_______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b都是正整数,且抛物线y=ax2+bx+l与x轴有两个不同的交点A、B.若A、B到原点的距离都小于1,则a+b的最小值等于( )
A. 16 B. 10 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F.

(1)求证:△DAC≌△EAB.
(2)求证:CD⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com